第四节  二次型及其标准形

一．数学概念

1. 二次型 

称含有n个变量 的二次齐次函数

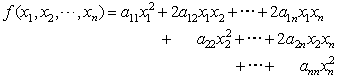
为二次型。

2. 二次型的矩阵形式

3. 二次型的秩

f的秩=R(A).

4. 二次型的标准形

称只含有平方项的二次型 为二次型的标准形(或法式)。

二．原理，公式和法则

1. 设可逆的线性变换x=Cy，将f化成标准形，即

其实质将对称矩阵A化成对角阵L。

2. 任给可逆矩阵C，令B=C^TAC，如果A为对称矩阵,则B也为对称矩阵，且R(B)=R(A)。

3. 任给二次型 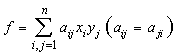，总存在正交变换x=Py，使f化成标准形 _，其中 是f的矩阵 的特征值。

三．重点、难点分析

本节的重点是用正交变换将二次型化成标准形，由于正交变换是保模的变换，所以正交变换将二次型化成标准形是今后用的最广的。难点是如何用正交变换将二次型化成标准形，其步骤较多，难度较大，但规律性很强，若抓住其规律，就容易将二次型化成标准形。

四．典型例题

例1 求一个正交变换x=Py，将 化成标准形，并写出其标准形。

解：①将f写成矩阵

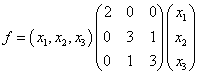
_{②求矩阵A的特征值}

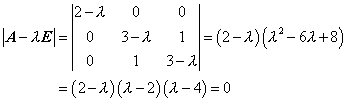
得A的全部特征值

③由 求A的特征向量

当 时，

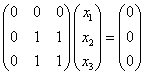
解之得特征向量

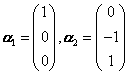
当 时，

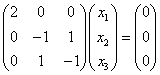
解之得特征向量

，

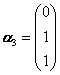④由于 已经正交,须单位化得

，

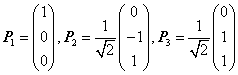⑤令 ，作x=Py为正交变换，将f化成标准形

对于二次型 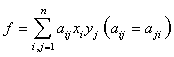化成标准型的一般步骤：

1 .将f写成矩阵形式 。

2 . 求A的全部特征值。

3 . 由 求A的特征向量。

4 . 不同的特征值所对应的特征向量已经正交，只须单位化 _；

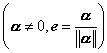对于k重特征值 所对应的k个线性无关的特征向量，用施密特标准正交化成两两正交的单位向量。

5. 把两两正交的单位向量拼成正交矩阵P，作正交变换x=Py，则x=Py把f化成标准形

_。