1.1 函数
一、数学概念
1. 函数的定义
设有两个变量x和y,如果对于x所考虑范围内的每一个值,y按一定规则对应着一个确定的值,则称y是x的函数,记作y=f(x).
2. 定义域
对于自变量x变化范围内的每一个值 ,函数y有一个确定的值与之对应,我们称函数在点 ,函数y有一个确定的值与之对应,我们称函数在点 处是有定义的,使函数有定义的点的全体(也就是x变化范围)称为函数的定义域. 处是有定义的,使函数有定义的点的全体(也就是x变化范围)称为函数的定义域.
3. 反函数
设函数y=f(x),当变量x在一个区域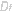 内变化时,变量y在区域 内变化时,变量y在区域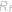 内变化,如果对于变量y在区域 内变化,如果对于变量y在区域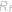 内任取一个值 内任取一个值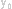 ,变量x在区域 ,变量x在区域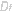 内有 内有 ,使 ,使 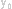 =f( =f( ),则变量x是变量y的函数,用x=φ(y)表示,函数x=φ(y)称为函数y=f(x)的反函数. ),则变量x是变量y的函数,用x=φ(y)表示,函数x=φ(y)称为函数y=f(x)的反函数.
4. 复合函数
两个函数的所谓复合,实际上就是中间变量介入自变量到因变量的变化过程.设有如下两个函数f:y=f(u),u∈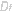 ,g:u=g(x),x= ,g:u=g(x),x=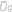 .若有 .若有  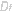 , 这样就可得复合函数y=f(g(x)),x∈ , 这样就可得复合函数y=f(g(x)),x∈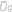 .由复合函数的定义可知,函数f和g能否构成复合函数f(g(x)),关键在于第二个函数的值域 .由复合函数的定义可知,函数f和g能否构成复合函数f(g(x)),关键在于第二个函数的值域 是否包含在第一个函数的定义域 是否包含在第一个函数的定义域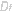 中,故有时候复合函数的定义域要小一些. 中,故有时候复合函数的定义域要小一些.
5. 基本初等函数
基本初等函数是指:幂函数、指数函数、对数函数、三角函数、反三角函数 .
6. 初等函数
由基本初等函数和常数经过有限次四则运算和复合运算而得到的能用一个解析表达式表示的函数都叫初等函数 .
上一页 下一页 下一页 |



