1.1.3 二次插值
线性插值仅仅利用了两个节点上的数据,插值结果的精度不高。下面考察二次Lagrange插值问题。
问题2 设已知三个互异节点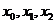 上的函数值为
上的函数值为
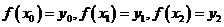 ,
,
求作一个形如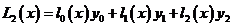 的二次式,使满足条件:
的二次式,使满足条件:
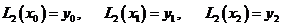
根据插值问题的存在唯一性,不妨令
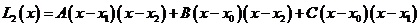
由条件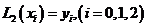 ,得
,得
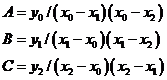
于是得到二次Lagrange插值公式:
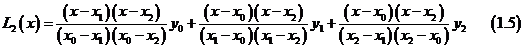
若记
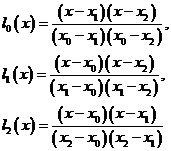
或统一写成
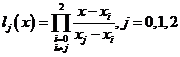
则可将二次Lagrange插值公式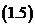 写成
写成
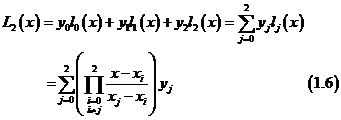
其中插值基函数 与线性插值基函数一样也具有如下性质:
与线性插值基函数一样也具有如下性质:
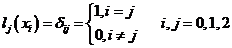 。
。
例2 利用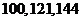 的开方值求
的开方值求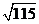 。
。
解 取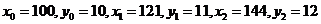 ,将
,将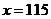 代入式
代入式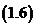 求得
求得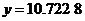 。与准确值
。与准确值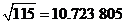 比较,这个插值结果有四位有效数字。
比较,这个插值结果有四位有效数字。

