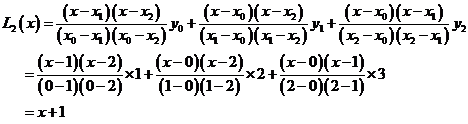1.1.4  次插值
次插值
现在考虑一般形式的Lagrange插值多项式。
问题3 设已知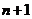 个互异节点
个互异节点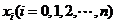 上的函数值
上的函数值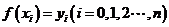 ,求作一个形如
,求作一个形如 的
的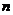 次式,使满足条件
次式,使满足条件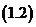 。其中,
。其中,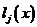 称为
称为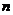 次Lagrange插值基函数。
次Lagrange插值基函数。
据插值问题的唯一性,并依据线性和二次Lagrange插值基函数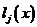 的性质,我们有理由推测:
的性质,我们有理由推测: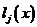 也应满足条件
也应满足条件
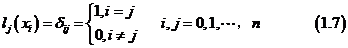
容易验证,在此条件下
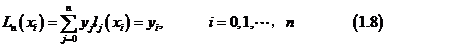
因此,问题3可归结为:构造满足条件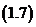 的
的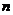 次式
次式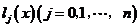 。
。
下面构造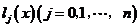 :
:
由条件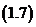 可知,
可知,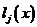 具有
具有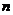 个零点
个零点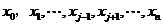 。因
。因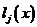 是
是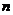 次式,故有
次式,故有
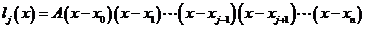
其中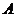 为待定的常数。由条件
为待定的常数。由条件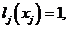 可得
可得
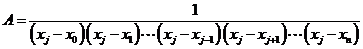
于是有
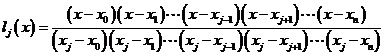
或写成
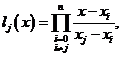
这样便有

称此式为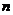 次Lagrange插值公式。引进记号:
次Lagrange插值公式。引进记号:
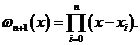
于是有
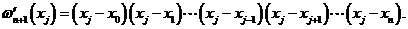
从而可将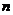 次Lagrange插值基函数
次Lagrange插值基函数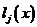 写成
写成
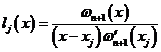
这时,式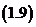 可改写为
可改写为
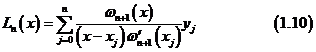
Lagrange插值公式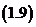 或
或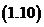 具有结构紧凑,便于在微机上实现的特点.
具有结构紧凑,便于在微机上实现的特点.
例3 求经过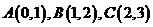 三个样点的插值多项式。
三个样点的插值多项式。
解 由题意可知,三个插值节点及对应的函数值为
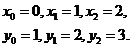
由二次Lagrange插值公式得