第一章
插值方法
实际问题中碰到的函数是各种各样的,有的表达式很复杂,有的甚至给不出数学式子,只是提供了一些离散数据,譬如某些点上的函数值和导数值。由于问题的复杂性,直接研究函数可能很困难。面对这种情况,一个很自然的想法是,设法将所考察的函数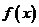 简单化,就是说,构造某个简单函数
简单化,就是说,构造某个简单函数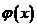 作为
作为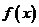 的近似,然后通过处理
的近似,然后通过处理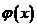 获得关于
获得关于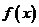 的结果。这类处理方法称为逼近方法。其中
的结果。这类处理方法称为逼近方法。其中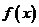 叫做被逼近函数,
叫做被逼近函数,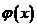 叫做逼近函数,两者之差
叫做逼近函数,两者之差
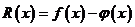
叫做逼近的误差或余项。插值方法是逼近方法的一种。如果要求逼近函数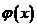 与被逼近函数
与被逼近函数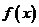 在一系列点
在一系列点 处的函数值或导函数值相等,即满足条件
处的函数值或导函数值相等,即满足条件
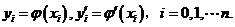
则这类逼近问题就是插值问题。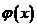 称为
称为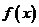 的插值函数,
的插值函数,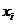 称为插值节点,
称为插值节点, 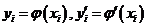 称为插值条件。一般说来,构造插值函数
称为插值条件。一般说来,构造插值函数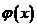 的办法很多,
的办法很多,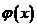 既可以是一个代数多项式或三角多项式,也可以是有理多项式;既可以是任意光滑函数,也可以是分段光滑函数。但通常使用的插值函数
既可以是一个代数多项式或三角多项式,也可以是有理多项式;既可以是任意光滑函数,也可以是分段光滑函数。但通常使用的插值函数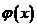 是多项式与样条函数。
是多项式与样条函数。
插值函数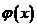 除了用于近似计算
除了用于近似计算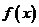 的函数值外,在数值积分,数值微分以及微分方程数值求解等领域中也有重要应用。
的函数值外,在数值积分,数值微分以及微分方程数值求解等领域中也有重要应用。
本章主要介绍多项式插值。这不仅是因为多项式简单,而且因为在许多情况下,函数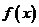 容易用多项式近似地表示出来。
容易用多项式近似地表示出来。
§1.1
Lagrange插值公式
1.1.1
插值问题的提法
设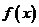 是实变量
是实变量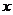 的单值函数,又设
的单值函数,又设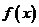 在
在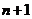 个互异节点
个互异节点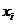 处的函数值
处的函数值
为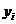
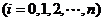 。我们的问题是:构造一个次数不超过
。我们的问题是:构造一个次数不超过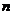 的多项式
的多项式
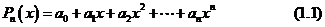
使 在节点
在节点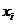 处满足条件
处满足条件
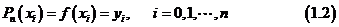
这个问题称为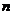 次代数插值问题。
次代数插值问题。
显然,为了确定满足条件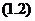 的多项式
的多项式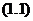 ,只需确定参数
,只需确定参数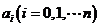 。由条件
。由条件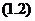 可知,参数
可知,参数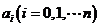 满足如下线性代数方程组:
满足如下线性代数方程组:
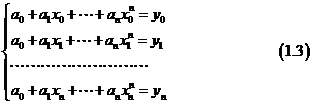
因为节点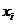 互异,所以该方程组的系数行列式不为零,故方程组
互异,所以该方程组的系数行列式不为零,故方程组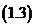 的解存在且唯一,即上述插值问题的解存在且唯一。所以我们有理由选择一条容易构造插值函数的途径。下面我们先给出插值问题的Lagrange形式。
的解存在且唯一,即上述插值问题的解存在且唯一。所以我们有理由选择一条容易构造插值函数的途径。下面我们先给出插值问题的Lagrange形式。

