检错纠错码

　　为了提高计算机的可靠性，除了采取选用更高可靠性的器件，更好的生产工艺等措施之外，还可以从数据编码上想一些办法，即采用一点冗余的线路，在原有数据位之外再增加一到几位校验位，使新得到的码字带上某种特性，之后则通过检查该码字是否仍保持有这一特性，来发现是否出现了错误，甚至于定位错误后，自动改正这一错误，这就是我们这里说的检错纠错编码技术。

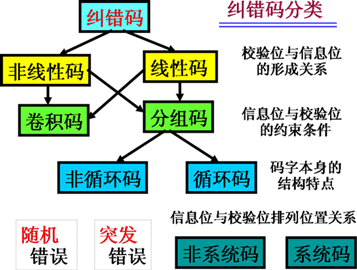
几种常用的检错纠错码

我们只介绍三种常用的检错纠错码： 奇偶检错码， 用于并行数据传送中 海明检错与纠错码，用于并行数据传送中 循环冗余码， 用于串行数据传送中

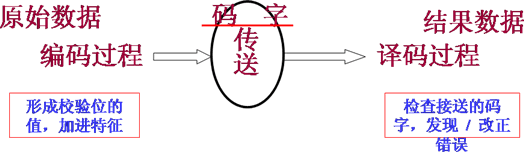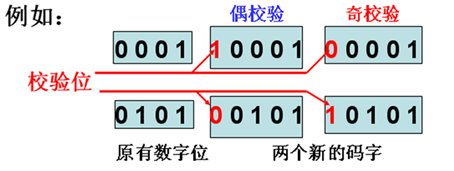
奇偶校验码

用于并行码检错 原理：在 k 位数据码之外增加 1 位校验位， 使 K+1 位码字中取值为 1 的位数总保持 为 偶数（偶校验）或 奇数（奇校验）。

奇偶校验码的实现电路

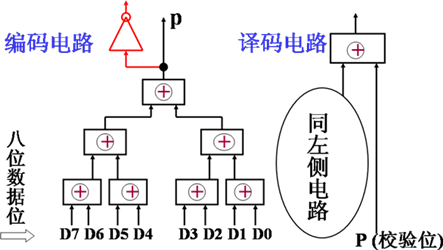
海明校验码

用于多位并行数据检错纠错处理
实现：为 k 个数据位设立 r 个校验位，
使 k+r 位的码字同时具有这样两个特性：
1.能发现并改正 k+r 位中任何一位出错，
2.能 发 现 k+r 位中任何二位同时出错，但已无法改正。

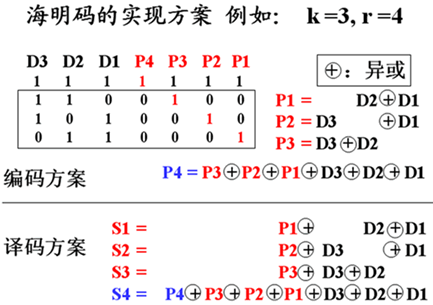
海明码的编码方法

　　合理地用 k 位数据位形成 r 个校验位的值，即保证用 k 个数据位中不同的数据位组合来形成每个校验位的值，使任何一个数据位出错时，将影响 r 个校验位中不同的校验位组合起变化。换言之，通过检查是哪种校验位组合起了变化，就能确定是哪个数据位错，对该位求反则实现纠错。
有时两位错与某种情况的一位错对校验位组合的影响相同，必须加以区分与解决。

检错纠错码小结

(1) K位码有2^K个编码状态，全用于表示合法码，则任何一位出错, 均会变成另一个合法码，不具有检错能力。
(2) 从一个合法码变成另一个合法码，只少要改变几位码的值，称为最小码距(码距)。
(3) K+1 位码，只用其2^K个状态，可使码距为2 ,如果一个合法码中的一位错了，就成为非法码，通过检查码字的合法性，就得到检错能力，这就是奇偶校验码。

检错纠错能力

(4) 对 k 位数据位，当给出 r 位校验位时， 要发现并改正一位错， 须满足如下关系：
2^ｒ> = k + r +1 ；
要发现并改正一位错，也能发现两位错,则应：
2^ｒ－１ >= k + r , 此时码距为 4。
(5) 若最小码距为 d (d>=2),
能发现 d-1 位错，或改正 (d-2)/2 (取整) 位错,要发现 l 位错,并改正 t 位错，应满足如下条件:
d >= l + t + 1 ( l >= t )