原码一位乘运算

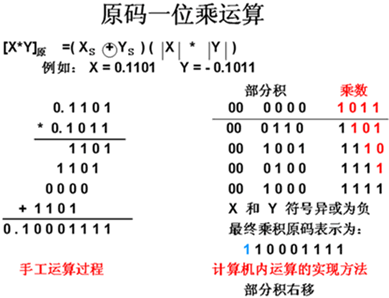
原码一位乘运算

例如： X = 0.1101 Y = - 0.1011
	问题： 1. 加法器只有两个数据输入端 2. 加法器与乘运算数据位数相同 解决方案： 每次求出部分积，而不是一次总累加 变每次左移被乘数为右移部分积 判乘数每一位的值用固定的一位线路 手工运算过程

实现原码一位乘法的逻辑线路图

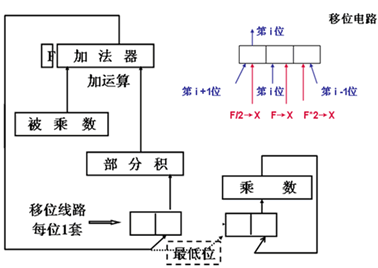
原码一位乘法

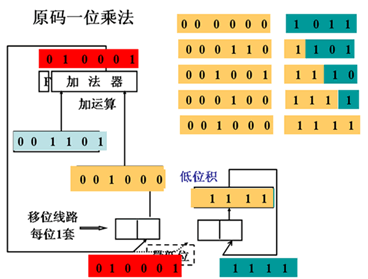
原码一位乘运算

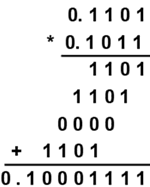
手工运算过程

手工运算过程

手工运算过程

手工运算过程

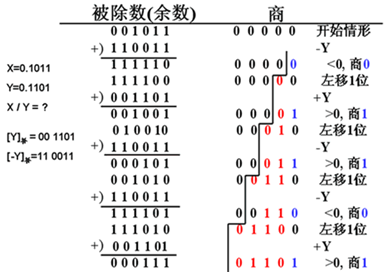
除法运算

　　在计算机内实现除运算时，存在与乘法运算类似的几个问题：
　　加法器与寄存器的配合，
　　被除数位数更长，商要一位一位地计算出来等。这可以用左移余数得到解决，且被除数的低位部分可以与最终的商合用同一个寄存器，余数与上商同时左移。

原码一位除运算

　　
　　原码一位除是指用原码表示的数相除，求出原码表示的商。除操作的过程中，每次求出一位商。
　　从理解原理考虑，用恢复余数除法讲解计算机内的实现方法更直观方便，即确定上商应为１还是为０时，必须用被除数或中间余数减去除数，通过检查本次求得的余数为正还是为负才能知道，而不象人计算时用眼睛直接看出来的。若求出一个为负的余数来，通常应首先恢复其值为正，再求下一位商才有道理。但计算机内从来不用这种办法，而是直接用求得的负余数求下一位商。

加减交替除法原理证明

１．若第i-1次求商余数为+R，商1余数左移得2R
２．则第i次求商R = 2R - Y
３．则第i+1次求商R = 2(R + Y) - Y = 2R + Y
实质是：对上次负差直接左移，本次用 +Y 求商即可。

实现原码一位除法运算的原理逻辑图

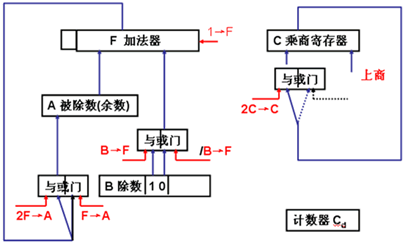
原码一位除运算