| |
| 一、正弦量的矢量表示法 |
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
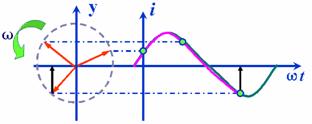
正弦信号的三要素可用一旋转矢量来表示:
令 矢量长度=Im
矢量初始角=Ψ
矢量旋转速度=ω
|
|
|
|
| |
|
如图
该矢量某一时刻在纵轴上的投影刚好等于正弦量的瞬时值。
将几个同频率的正弦量用相应的矢量表示并画在同一坐标平面上,这样的图叫做矢量图。
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| 二、正弦量的相量表示法 |
|
|
|
|
|
|
|
|
| |
|
一般我们研究的是同频率的正弦量,
用相量表示时,它们同以ω速度旋转,相对位置保持不变。因此,在同一相量图中,以t=0时刻的相量表示正弦量。
相量的写法为:大写字母的上方加一个“.”。
我们知道一个相量可以用复数表示,而正弦量又可以用相量表示,因此正弦量可以用复数表示。
|
| |
1. 复数表示法: |
|
|
|
|
 |
|
| |
|
|
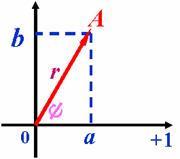
A=
a+j b 代数式
A= r(cosψ +j sinψ ) 三角式
根据欧拉公式:
ejψ=
cosψ+ j sinψ
A = r ejψ
指数式
A = r∠ψ 极坐标式
其中
a = r cosψ b = r sinψ
ψ= arctg ( b/a )
|
|
|
|
|
|
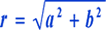 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|



