 |
 |
 |
 |
 |
 |
 |
 |
|
 |
|
 |
|
| 第一节 线面比较法消除隐藏线 | ||||
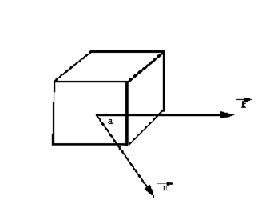
设空间有一个四面体，顶点A，B，C，D的坐标依次是（0，0，0），（2，0，1），（4，0，0）,(3,2,1)从z轴正向无穷远处观察,求各面的可见性。 观察方向向量是k=(0,0,1),三角面DAB的法向量是: 因此, 
，面DAB为可见面.类似计算可知，面DBC是可见面,面ADC是不可见面,面ACB退化为线。
利用外法线就可以判断凸多面体上各表面的可见性，由此就能解决对单个凸多面体的隐藏线和隐藏面的消除问题。 消除隐藏线的线面比较法的最先一步就是利用外法线判断出所有可能的可见面，可能可见面上的线段是可能可见线。要依次用每一条可能可见线，与每一个可能可见面比较，从而确定出可见线、隐藏线及可见线上的隐藏部分。 |
||||
 第一节
线面比较法消除隐藏线第二节
曲面隐藏线消除的浮动水平线算法第三节
深度排序算法第四节
z-缓冲算法 第五节
扫描线算法第六节
区域分割算法 |
