| |
 曲线和曲面参数表示 曲线和曲面参数表示
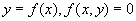
(1)与坐标轴相关的,不便于进行坐标变换;
(2)会出现斜率为无穷大的情况;
(3)难以灵活地构造复杂的曲线、曲面
(4)非参数的显示方程只能描述平面曲线,空间曲线必须定义为两张柱面与的交线。
(5)假如我们使用非参数化函数,在某个xoy坐标系里一条曲线,一些x值对应多个y值,而一些y值对应多个x值。
在空间曲线的参数表示中,曲线上每一点的坐标均要表示成某个参数t的一个函数式,则曲线上每一点笛卡尔坐标参数式是:
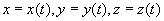
把三个方程合写到一起,曲线上一点坐标的矢量表示是:
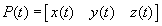
关于参数t的切矢量或导函数是:
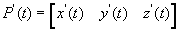
曲面写为参数方程形式为:

曲线或曲面的某一部分,可以简单地用a≤t≤b界定它的范围。
 直线段 直线段
端点坐标分别是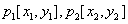 ,直线段的参数表达式是: ,直线段的参数表达式是:

参数表示相应的x,y坐标分量是:
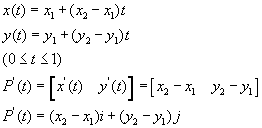
|
|
|



