 |
 |
 |
 |
 |
 |
 |
 |
|
 |
|
 |
|
| 第六节 区域分割算法 | ||||
4.
有多于一个的包围的、相交的或被包围的多边形，且至少有一个包围的多边形。检查是否能有一个包围的多边形，它位于所有其它多边形的前面。如果有，就可以让整个区域都填充为这个多边形的象素值。具体的检查方法是，对所有的多边形，计算其所在平面在区域的四个角点的应有深度，即相应的z坐标，如果有一个包围的多边形的响应四个z坐标，都小于其它多边形的对应z坐标，那么这个包围的多边形就位于所有其它多边形的前面。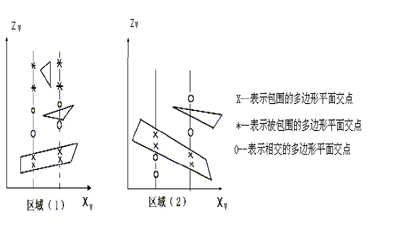
情形4的两种情形 区域经过分割变小以后，只需要考虑包含的多边形和相交的多边形的变化。 因为分离的或包围的多边形，对变小的区域，仍然保持是分离的或包围的。分割进行到达到显示设备的分辨能力之后就可以停止，即最小的区域可以是显示表面上的一个象素单位。如果在做了准备做的最大数目的分割之后，仍然不能做出应该如何填充的决定，那么，就计算所有有关多边形在这个不可再分区域对应的点的范围的中心处的z坐标值，取z坐标最小的多边形象素值填充这个区域。 Wanock首先提出的最初的区域分割算法是每次把区域分成四个正方形。下图所示是对一个投影是一个三角形和一个长方体的场景，做了5次区域分割的情形，其中区域内标出的数字，表示可以作出决定的前面所说的四种情形中的哪一种。没有标出数字的区域是还不能做出决定。 |
||||
 第一节
线面比较法消除隐藏线第二节
曲面隐藏线消除的浮动水平线算法第三节
深度排序算法第四节
z-缓冲算法 第五节
扫描线算法第六节
区域分割算法 |
