第5章 地基中的应力计算

5.4 地基附加应力
 
    线荷载作用下的地基附加应力－弗拉曼（Flamant）解
    在半空间表面无限长直线上，作用一个竖向均布线荷载。求在地基中任意点M处引起的附加应力。设一个竖向线荷载p (kN/m)作用在y座标轴上，则沿y轴某微分段dy上的分布荷载以集中力dP=pdy代替，从而求得地基中任意点M处由P引起的附加应力dsz为：
                
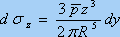
    积分求得M点的sz:
            
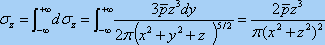
    同理，按上述方法可推导出：
                
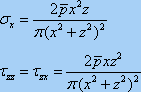
    均布竖向条形荷载
    当地基表面宽度为b的条形面积上作用着竖向均布荷载p0(kPa)，此时,地基内任意点M的附加应力sz可利用弗拉曼解和积分的方法求得。首先在条形荷载的宽度方向上取微分段dx，将其上作用的荷载视为线荷载，则在M点引起的竖向附加应力dsz为:
    
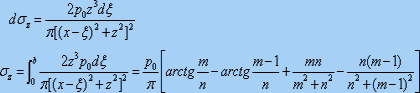
定义Ksz，Ksx，Ksxz分别为均布竖向条形荷载下的竖向附加应力系数、水平向附加应力系数和附加剪应力系数， 则

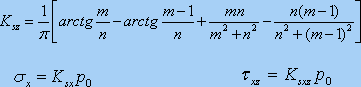
需注意的是，条形基础下求地基内的附加应力时，必须注意坐标系统的选择。
    均布条形荷载下地基中附加应力的分布规律
    1．σz不仅发生在荷载面积之下，而且分布在荷载面积以外相当大的范围之下，这就是所谓地基附加应力的扩散分布。
    2．在离基础底面不同深度z处各个水平面上，以基底中心点下轴线处的σz为最大，随着距离中轴越远越小。
    3．在荷载分布范围内任意点沿垂线的σz值，随深度越向下越小。
    三角形分布的竖向条形荷载
    当地基表面宽度为b的条形面积上作用着最大强度为pt的三角形分布荷载，首先在条形荷载的宽度方向上取微分段dx，将其上作用的荷载 　　　　　视为线荷载，此时，可利用弗拉曼解和积分的方法求得地基内任意M点处的附加应力sz为：

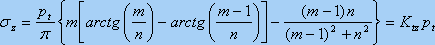
    式中 Ktz为三角形分布荷载附加应力系数。其值可按m＝x/b和n=z/b的数值查表得到。
    均布水平条形荷载
    地基表面宽度为b的条形面积上作用一强度为ph的水平均布荷载，如图，则任一点M所引起的地基附加应力可由弹性理论表示，通过沿整个宽度积分，可得到M点的竖向附加应力

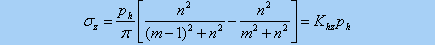
式中 Khz为水平均布条形荷载附加应力系数。

| 5.1 | 5.2 | 5.3 | 5.4 | 5.5 | 上一页 | 下一页 |