| |
 参数连续性 参数连续性
一函数在某一点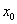 处具有相等的直到k阶的左右导数,称它在 处具有相等的直到k阶的左右导数,称它在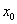 处是k次连续可微的,或称它在 处是k次连续可微的,或称它在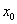 处是k阶连续的,记作 处是k阶连续的,记作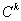 。几何上 。几何上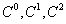 依次表示该函数的图形、切线方向、曲率是连续的。 依次表示该函数的图形、切线方向、曲率是连续的。
 几何连续性 几何连续性
两曲线段的相应的弧长参数化在公共连接点处具有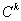 连续性,则称它们在该点处具有k阶几何连续性,记作 连续性,则称它们在该点处具有k阶几何连续性,记作 。零阶几何连续
。零阶几何连续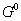 与零阶参数连续 与零阶参数连续 是一致的。一阶几何连续 是一致的。一阶几何连续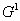 指一阶导数在两个相邻曲线段的交点处成比例,即方向相同,大小不同。二阶几何连续 指一阶导数在两个相邻曲线段的交点处成比例,即方向相同,大小不同。二阶几何连续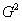 指两个曲线段在交点处其一阶和二阶导数均成比例。 指两个曲线段在交点处其一阶和二阶导数均成比例。
 光顺 光顺
光顺(smoothness)是指曲线的拐点不能太多,要光滑顺畅。对于平面曲线相对光顺的条件应该是:(1)具有二阶几何连续(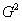 );(2)不存在多余拐点和奇异点;(3)曲率变化较小。 );(2)不存在多余拐点和奇异点;(3)曲率变化较小。
|
 |
|
|



