 |
 |
 |
 |
 |
 |
 |
 |
|
 |
|
 |
|
| 第五节 简单多边形的三角剖分 | |||
| 简单多边形做三角剖分,是要求选出完全在内部又互不相交的一组对角线，把整个多边形划分成一些三角形。这里对角线是不相邻顶点间的连线,选出的对角线的集合称为是简单多边形的三角剖分。 对任意一个简单多边形,其三角剖分不是唯一的。 事实1 简单多边形必有一条对角线完全在其内部。 事实2 简单多边形上必有连续的三个顶点A,B,C,使对角线AC完全在其内部。 |
|||
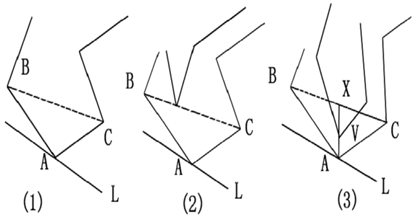 必有完全在内部的对角线 |
|||
| 简单多边形三角剖分的算法:考查连续三个顶点A,B,C,若AC完全在多边形内部,则可输出△ABC为一个剖分后形成的三角形,删除点B后再对少了一个顶点的多边形继续进行。 简单多边形的顶点序列为  ,那么算法可描述如下: |
|||
 第一节
线段的交点计算第二节
多边形表面的交线计算第三节
平面中的凸壳算法第四节
包含与重叠第五节
简单多边形的三角剖分 |
