 |
 |
 |
 |
 |
 |
 |
 |
|
 |
|
 |
|
| 第三节 平面中的凸壳算法 | ||||
 凸壳
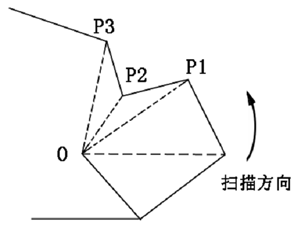
凸壳指包含一个平面点集的最小凸区域。 凸区域指要求区域内任意两点的连线仍在该区域内。 设S是平面上n个点的集合,则S的凸壳是一个凸多边形,它包含所有n点且面积最小。事实上求点集S的凸壳就是要在S中选出壳上的点并排出围成凸多边形的次序。 Graham扫描算法
处理的思路是设想有一内点O并且不妨设想O就是坐标原点,这时点集S中所有各点相对轴OX有一个倾角。所有各点按倾角递增排序后,如果某一点不是壳上顶点,则它必然在两个壳顶点与点O形成的三角形内部。 Graham扫描的实质是围绕已经按"倾角"排序的各顶点进行一次扫描,在扫描过程中消去在凸壳内部的点,留下以希望次序排列的壳顶点。 |
||||
 |
||||
由于是按倾角递增排序,可知若连续三个顶点 是一个“右转”，则 是一个应去掉的内点。
|
||||
 第一节
线段的交点计算第二节
多边形表面的交线计算第三节
平面中的凸壳算法第四节
包含与重叠第五节
简单多边形的三角剖分 |
