 |
 |
 |
 |
 |
 |
 |
 |
|
 |
|
 |
|
| 第三节 平面中的凸壳算法 | ||||
对给出的三点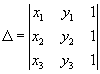
,设它们的坐标是 ,这时要判断三点在 处形成一个右转还是左转,可以计算下面的行列式
其中△给出的是带有正负号的三角形  面积的2倍,因此若△>0,则是左转;
△<0,则是右转;
△ =0,则三点共线。 实现此算法可选点集S中x坐标最小的点为内点O,设想过O有一条向右的射线,对其余各点,相对该射线计算倾角然后再排序。  Graham扫描算法
1.〔倾角排序〕选出输入点集S中x坐标最小的点,若这样的点不唯一则再由其中选出y坐标最小的点,设为O。设想有一条从O向右的射线OX,对点集中其余每一点P,计算倾角POX,再按倾角排序,得点序列  ;2.〔准备扫描〕  ;
3.〔扫描〕若NEXT(v)≠Q1,则循环执行下面操作,至NEXT(v)=Q1时止,此时点序列中剩下排成凸多边形的壳上顶点,算法结束。 若三个相继的点v,NEXT(v),NEXT(NEXT(v))形成一个左转,则v←NEXT(v);否则,先删除NEXT(v),再做v←PRED(v); NEXT(v)和PRED(v)是两个函数,其值分别为算法操作的点序列中v的下一点和前一点。这里取下一点和前一点时认为点序列是首尾相接的,即若v是点序列中第一点,则PRED(υ)是点序列中最后一点;若v是最后一点,NEXT(v)是第一点。 |
||||
 |
||||
 第一节
线段的交点计算第二节
多边形表面的交线计算第三节
平面中的凸壳算法第四节
包含与重叠第五节
简单多边形的三角剖分 |
