 |
 |
 |
 |
 |
 |
 |
 |
|
 |
|
 |
|
| 第五节 简单多边形的三角剖分 | |||
| 事实3
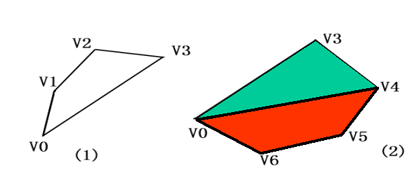
在n边形(n≥3)的任意一种三角剖分中,每一对相邻顶点中至少有一个顶点是某条对角线的端点。 因为若相邻顶点  , 都不是某条对角线的端点,则区域( ,,, )中没有对角线,因而也就没有被三角剖分。事实4 如果  是三角剖分的一条对角线,则一定存在某顶点 ,使得和是多边形的边或对角线。因为若不然,一定存在以 为边界的某个区域没有被三角剖分。
顶点序列  确定的凸n边形的最小三角剖分挑选两个相邻顶点比方选  和 ,由事实3知道在最小三角剖分中,必有另一顶点,或者使是对角线,或者使是对角线。对有n个顶点的多边形， 的选取方法有n-3种。对于每个可能的 用对角线(或)把原多边形剖分成两个较小的多边形,这样原问题就被分成为两个子问题。往下需要寻找分成的两个较小凸多边形的最小三角剖分。（递归） 选择剖分方法,使得每次剖分后所得的子问题只涉及一条原多边形的对角线。 由事实4知在最小剖分中的对角线一定与另外一点构成三角形。 |
|||
 |
|||
 第一节
线段的交点计算第二节
多边形表面的交线计算第三节
平面中的凸壳算法第四节
包含与重叠第五节
简单多边形的三角剖分 |
