第一节
运输问题 (1)
(2)
若总产量等于总销量(产销平衡),试确定总运费最省的调运方案。
建模:设xij表示从产地Ai到销地Bj的运量(i=1,2, …,m;j=1,2,
…,n) 则运输问题的数学模型如下:
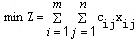
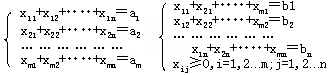
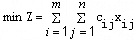
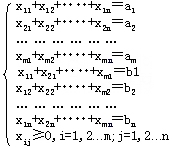
显然,模型是具有m×n个变量,m+n个约束的线性规划,可以用一般的单纯形法求解,但是当m与n较大时,模型的规模比较大,计算比较困难。为了进一步研究针对运输问题的特殊解法,下面考察它的约束系数矩阵。记
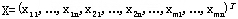
则 
A是m+n行,m×n列的矩阵,它比较稀疏,除有2m×n个1以外,其余元素皆为0,变量Xij对应的系数列向量Pij中,除第i个和第m+j个为1外,其余都为0,即
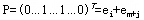
容易证明,秩A=m+n-1 事实上,由于A的前m行之和恰好等于后n行之和,因此,
秩A≤m+n-1;又,取A的前m+n-1行, 变量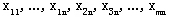 对应的列所构成的A的子式为 对应的列所构成的A的子式为
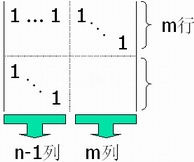

由此易知,这个m+n-1阶子式的值为1或-1,所以,A的秩恰为m+n-1。可见,运输问题的基可行解中,基变量的个数应为m+n-1个。
由于运输问题的数学模型具有以上特点,所以求解运输问题时,可以采用比较简单的计算方法——表上作业法。
|

