第一节 对偶问题
    对偶理论是线性规划的内容之一。任何一个线性规划都有一个伴生的线性规划，称之为原规划的对偶规划问题。下面通过实例引出对偶问题，然后给出对偶线性规划的定义。
    第一章例1提出的线性规划问题为：某工厂生产Ⅰ、Ⅱ两种型号计算机，每生产一台Ⅰ型和Ⅱ型计算机所需的原料、工时和提供的利润以及资源的限制量如下表：
        
    试确定获利最大的生产方案。
    该问题的线性规划数学模型为：
        
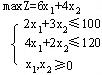
    假如现在工厂自己不生产产品Ⅰ、Ⅱ，而将可利用的资源都出让给其它企业，试确定这些资源的最低可接受价格。最低可接受价格是指按这种价格转让资源比自己生产产品Ⅰ、Ⅱ合算的价格。
    设y1,y2,为这两种资源的价格，为了使工厂出让资源合算，显然应该使出让原来生产一台产品Ⅰ的资源所得收入不低于自己生产一台产品Ⅰ的利润，即 2y1+4y2≥6 对于产品Ⅱ，同样可以建立类似的约束条件 3y1+2y2≥4 显然在满足这两个约束的前提下，价格越高，该工厂越合算，但价格太高，接受方面又不会愿意购买。因此，我们需要确定的价格是 使工厂合算的最低价格，故应建立目标函数： minW=100y1+120y2
综上所述，出让资源问题的数学模型如下：
        
    工厂决策者所面临的两个问题的数学模型都是线性规划，它们在结构上具有某种对称性，称后一个线性规划为原规划的对偶问题。
    定义 称线性规划
    为原线性规划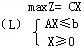
    的对偶规划问题。