第四节
对偶单纯形法 (1) (2)
在单纯形法中,原问题的最优解满足:
(1)是基本解;
(2)可行( 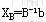 ≥0); ≥0);
(3)检验数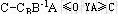 ,即对偶解可行。
,即对偶解可行。
单纯形算法是从满足(1)、(2)的一个基可行解出发,转换到另一个基可行解,一直迭代到(3)得到满足,即对偶解可行为止。而对偶单纯形法则是从满足(1)、(3)的一个对偶可行解出发,以基变量值是否全非负为检验数,连续迭代到(2)得到满足,即原问题的基解可行为止。两种算法结果是一样的,区别是对偶单纯形法的初始解不一定可行,只要求所有检验数都非正,在保证所得解始终是对偶可行解的前提下,连续迭代到原问题的基解可行,从而取得问题的最优解。
对偶单纯形法计算步骤如下:
步骤1 确定原问题(L)的初始基B,使所有检验数 ,即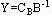 是对偶可行解,建立初始单纯形表。 是对偶可行解,建立初始单纯形表。
步骤2 检查基变量的取值,若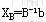 ≥0,则已得最优解,计算停;否则求 ≥0,则已得最优解,计算停;否则求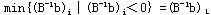
确定单纯形表第L行对应的基变量为旋出变量。
步骤3 若所有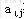 ,则原问题无可行解,计算停;否则,计算 ,则原问题无可行解,计算停;否则,计算
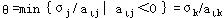
确定对应的为Xk旋入变量。
步骤4 以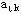 为主元作(L,K)旋转变换,得新的单纯形表,转步骤2。 为主元作(L,K)旋转变换,得新的单纯形表,转步骤2。
可以证明,按上述方法进行迭代,所得解始终是对偶可行解。
|

