第五节
灵敏度分析 (1) (2)
(3) (4) (5)
(6) (7)
在线性规划问题中,目标函数、约束条件的系数以及资源的限制量等都当作确定的常数,并在这些系数值的基础上求得最优解。但是实际上,这些系数或资源限制量并非一成不变的,它们是一些估计或预测的数字,比如价值系数随着市场的变化而变化,约束系数随着工艺的变化或消耗定额的变化而变化,计划期的资源限制量也是经常变化的。当这些系数发生变化时,最优解会受到什么影响?最优解对哪些参数的变动最敏感?搞清这些问题会使我们在处理实际问题时,具有更大的主动性和可靠性。
分析线性规划模型的某些系数或限制数的变动对最优解的影响,被称作灵敏度分析。
灵敏度分析主要解决两个问题:
⑴这些系数在什么范围内变化时,原先求出的最优解或最优基不变?即最优解相对参数变化的稳定性。
⑵如果系数的变化引起了最优解的变化,如何用最简便的方法求出新的最优解。
下面分别介绍各类参数变化的灵敏度分析。
5.1 目标函数中价值系数C的分析
分别就非基变量和基变量的价值系数两种情况来讨论:
⒈设非基变量Xj的价值系数Cj,有增量△Cj,其它参数不变,求△Cj的范围使原最优解不变。由于Cj是非基变量的价值系数,因此它的改变仅仅影响检验数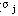 的变化,而对其它检验数没有影响。 的变化,而对其它检验数没有影响。
由 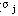 +△Cj≤0
知,当△Cj≤- +△Cj≤0
知,当△Cj≤-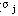 时,原最优解不变。
时,原最优解不变。
⒉设基变量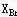 的价值系数 的价值系数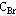 有增量△ 有增量△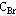 ,其它参数不变,求△ ,其它参数不变,求△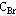 的范围使原最优解不变。 的范围使原最优解不变。
由于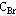 是基变量的价值系数,因此它的变化将影响所有非基变量检验数的变化。 是基变量的价值系数,因此它的变化将影响所有非基变量检验数的变化。
由新的非基变量检验数:
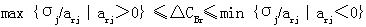 ,可知,当
,可知,当 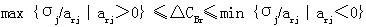 时,原最优解不变。 时,原最优解不变。
|

