第五节
灵敏度分析 (1) (2)
(3) (4) (5)
(6) (7)
2.增加一个新约束条件的分析
设 是新增加的约束条件,试分析原问题最优解有无变化?将原最优解代入新约束中,如果满足新约束条件,则原最优解不变,反之,则需进一步求出新的最优解。 是新增加的约束条件,试分析原问题最优解有无变化?将原最优解代入新约束中,如果满足新约束条件,则原最优解不变,反之,则需进一步求出新的最优解。
考虑到单纯形算法中,每步迭代得到的单纯形表对应的约束方程组都与原约束方程组等价,因此,可以将新约束方程 增填到原最优表的下面,变化后的单纯形表增加一个行、一个列,新约束对应的基变量是
增填到原最优表的下面,变化后的单纯形表增加一个行、一个列,新约束对应的基变量是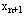 ,在单纯形表中,由于增加了新约束,原基变量对应的列向量可能不再是单位列向量,所以需用初等行变换将表中基变量对应的列向量变为单位列向量。变换后,原最优表的检验数不变,但基变量
,在单纯形表中,由于增加了新约束,原基变量对应的列向量可能不再是单位列向量,所以需用初等行变换将表中基变量对应的列向量变为单位列向量。变换后,原最优表的检验数不变,但基变量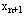 所取的值一般要变了。若 所取的值一般要变了。若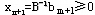 ,则已得最优解;反之,若 ,则已得最优解;反之,若
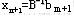 <0,则用对偶单纯形法继续求解。 <0,则用对偶单纯形法继续求解。
例6 设第一章例1的原线性规划问题中增加一道加工工序,需要在另一台设备上进行。已知每台Ⅰ、Ⅱ型产品在该设备上加工工时分别为2,3个单位,计划期内该设备总台时为90单位,试分析原最优解有无变化?如果有变化,求出新的最优解。
解:新工序对应的约束条件为 2X1+3X2≤90
将原问题最优解 X1=X2=20,代入该约束左端,显然不满足约束条件,因此原最优解不再是最优解。
将 2X1+3X2+X5=90 增填到原最优表的下面,用初等行变换及对偶单纯形法计算,结果如下:
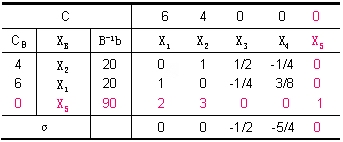
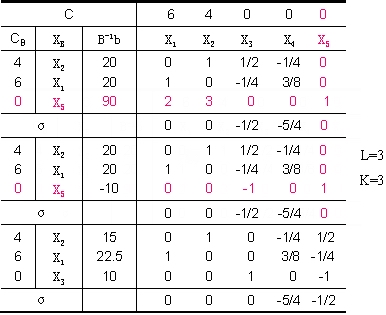
由此得最优解:X1=22.5,X2=15,X3=10,X4=X5=0
最优值:Z﹡=195 |

