第五节
灵敏度分析 (1) (2)
(3) (4) (5)
(6) (7)
3.改变某非基变量的系数列向量的分析
设非基变量Xj的系数列向量变为Pj′,试分析原最优解有何变化。
该变化只影响最优单纯形表的第j列及其检验数。因此,可以先计算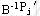 及 及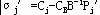 , ,
若 ≤0,则原最优解不变,反之,若 ≤0,则原最优解不变,反之,若 >0,则以 >0,则以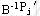 替代原最优表的第j列,用单纯形法继续求解。 替代原最优表的第j列,用单纯形法继续求解。
4.改变某基变量的系数列向量的分析
设基变量Xj的系数列向量变为Pj′,试分析原最优解有何变化。
显然,Pj的变化将导致B的变化,因而原最优表的所有元素都将发生变化,似乎只能重新计算变化后的模型。但是,经过认真分析,还是可以利用原最优解来计算新最优解的。
我们可以将Xj看作新增加的变量,用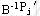 替代原最优表的第j列(单位列向量),然后再利用初等行变换将表中的 替代原最优表的第j列(单位列向量),然后再利用初等行变换将表中的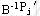 恢复到原来的单位列向量,并重新计算检验数。则变化后的单纯形表有以下几种情况: 恢复到原来的单位列向量,并重新计算检验数。则变化后的单纯形表有以下几种情况:
1°基变量取值全非负,且检验数全非正,已得新的最优解。
2°基变量取值全非负,但存在正的检验数,该解是基可行解,可以用单纯形法继续求解。
3°存在取负值的基变量,但检验数全非正,该解是对偶可行解,可以用对偶单纯形法继续求解。
4°存在取负值的基变量,且存在正的检验数,该解既不是基可行解,又不是对偶可行解。
对于这种情况,我们将表中取负值的基变量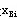 对应的行还原成约束方程,用-1乘方程两端,再在方程左端加一个人工变量 对应的行还原成约束方程,用-1乘方程两端,再在方程左端加一个人工变量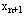 ,用该方程替代原单纯形表的第i行,则表中第i行对应的基变量为人工变量 ,用该方程替代原单纯形表的第i行,则表中第i行对应的基变量为人工变量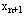 ,其对应的数值为 ,其对应的数值为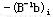 ,其价值系数为-M。然后可以用单纯形法继续求解。
,其价值系数为-M。然后可以用单纯形法继续求解。 |

