第五节
灵敏度分析 (1) (2)
(3) (4) (5)
(6) (7)
5.2 资源系数b的分析
设bi有增量△bi,其它参数不变,则bi的变化将影响基变量所取的值,但对检验数没有影响,记新的基变量为
,则
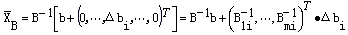
这里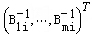 是原最优基逆阵 是原最优基逆阵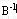 的第i列。如果变化后仍有 的第i列。如果变化后仍有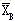 ≥0,则原最优基不变。由此可知,当△bi满足 ≥0,则原最优基不变。由此可知,当△bi满足
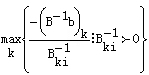 ≤△bi≤
≤△bi≤ 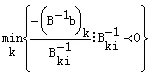
时,原最优基不变。
结果说明 ,△bi的变化范围是由原基变量的相反数与B-1的第i列元素的比值所确定的。
如果△bi不在上述范围变动,则变化后的基变量所取值 肯定会出现负分量,但由于△bi不影响检验数的变化,因此可以用 取代原最优解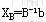 ,以该解为初始解,用对偶单纯形法继续求解。
,以该解为初始解,用对偶单纯形法继续求解。
例4 已知线性规划问题的初始解及最优解见例3。
⑴求△bi的范围,使原最优基不变;
⑵若bi变为200,试求新的最优解。
解:⑴由已知单纯形表可知
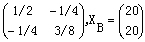
用基变量的负值与的第一列相应元素去比,得 -40≤△bi≤80 时,原最优基不变。
⑵变化后基变量的取值为 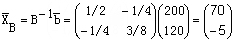
不是可行解,须用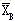 替换原最优表中基变量的值,并采用对偶单纯形法继续求解,结果如下: 替换原最优表中基变量的值,并采用对偶单纯形法继续求解,结果如下:
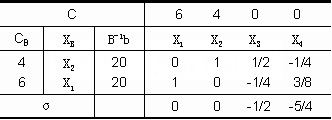
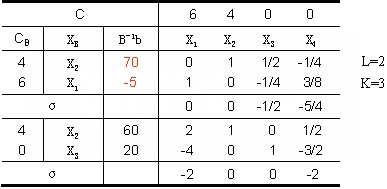
由此得最优解:X1=0,X2=60,X3=20,X4=0
最优值:Z﹡=240 |

