第五节
灵敏度分析 (1) (2)
(3) (4) (5)
(6) (7)
5.3 系数矩阵A的分析
以下分4种情况讨论系数矩阵的变化。
1.增加一个新变量的分析
设是新增加的变量,其对应的系数列向量为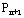 ,价值系数为 ,价值系数为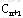 ,试讨论原最优解有无改变?及如何尽快地求出新的最优解。 ,试讨论原最优解有无改变?及如何尽快地求出新的最优解。
如果原问题增加一个新变量,则系数矩阵增加一个列,注意到新增加的列在以B为基的单纯形表中应变为
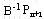 ,所以可先计算 ,所以可先计算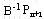 及 及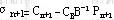 ,若σn+1≤0,则原最优解不变,反之可将 ,若σn+1≤0,则原最优解不变,反之可将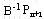 增填到原最优表的后面,用单纯形法继续迭代。 增填到原最优表的后面,用单纯形法继续迭代。
例5 设第一章例1的原线性规划问题中考虑生产Ⅲ型计算机,已知生产每台Ⅲ型计算机所需原料4个单位,工时3个单位,可获利润8个单位。试问该厂是否
应该生产 Ⅲ型计算机?如果生产,应该生产多少?
解:设生产Ⅲ型计算机X3′台,由原最优基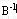 的逆可得: 的逆可得:
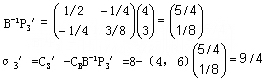
因为σ3′>0,所以安排生产Ⅲ型计算机有利,将 P3′增填到原最优表的后面,并用单纯形法继续计算,结果如下: P3′增填到原最优表的后面,并用单纯形法继续计算,结果如下:
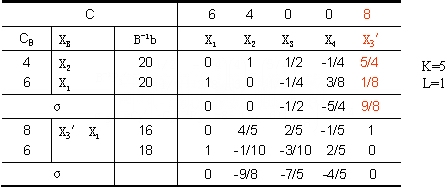
最优解;X1=18,X2=0,X3=0,X3′=16,X4=0
最优值:Z﹡=236 |

