第四节
对偶单纯形法 (1) (2)
例2 用对偶单纯形法求解下述问题
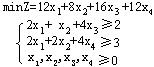
解:令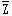 =-Z,则问题可变为
=-Z,则问题可变为
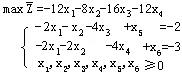
取B=(P5,P6)为初始基,易见所有检验数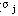 ≤0, ≤0,
从而可建立单纯形表,计算结果如下:
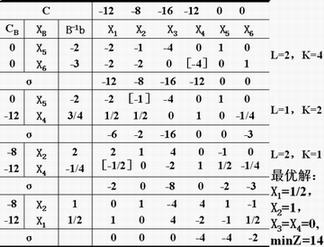
本例如果用单纯形法计算,确定初始基可行解时需引入两个人工变量,计算量要多于对偶单纯形法。一般情况下,如果问题能够用对偶单纯形法计算,计算量会少于单纯形法。但是,对偶单纯形法并不是一种普遍算法,它有一定的局限性,不是任何线性规划问题都能用对偶单纯形法计算的。当线性规划问题具备下面条件时,可以用对偶单纯形法求解:
①问题标准化后,价值系数全非正;
②所有约束全是不等式。 |

