第二节
表上作业法 (1) (2)
(3) (4) (5)
表上作业法的思想和单纯形法类似,即首先确定一个初始方案,也就是找出一个基可行解,然后根据判别准则来检查这个初始方案是不是最优的,如果不是最优的,那么对该方案进行调整,直至求出最优方案止。下面介绍它的计算步骤。
2.1 确定初始调运方案
确定初始调运方案的方法很多,我们介绍两种:最小元素法和西北角法。
1.最小元素法
这个方法的基本思想是就近供应,即从运价表中最小运价开始确定调运量,然后次小,一直到给出初始调运方案为止。具体操作方法如下:
1°找出运价表中最小元素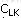 ,确定 ,确定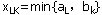 ,若 ,若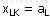 ,则令 ,则令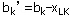 ,划掉运价表的第L行;反之,若 ,划掉运价表的第L行;反之,若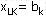 ,则令
,则令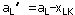 ,划掉运价表的第K列。 ,划掉运价表的第K列。
2°在运价表剩余元素中重复1°,直至运价表中元素全被划掉止。
例1 某糖果公司下设三个工厂,每日产量分别为:A1—7吨,A2—4吨,A3—9吨。该公司将这些产品运往四个门市部,各门市部每日销售量为:B1—3吨,
B2—6吨, B3—5吨, B4—6吨。各工厂到各门市部的单位运价见表3-1,试确定总运费最省的调运方案。
表3-1
单位运价表
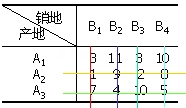
解:先用最小元素法确定初始调运方案。画出产销平衡表: 表3-2
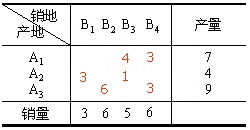
用最小元素法所得初始调运方案如表3-2红字所示。称产销平衡表中填有数字的格为数字格,没填数字的格称为空格。由最小元素法可知,在产销平衡表上每填一个数字,就划去一个行或列,表中共有m行n列,用m+n-1条线就可划去运价表所有元素,相应地在产销平衡表上就形成m+n-1个数字格。前面已经论证了运输问题的约束系数矩阵A的秩恰为m+n-1,理论上可以证明,这些数字格所所对应的变量相当于基变量,而空格对应的变量相当于非基变量,用最小元素法得到的初始调运方案构成一个基可行解。
特别要注意的是:当最小运价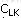 对应的产量 对应的产量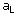 与销量
与销量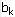 相等时,在产销平衡表填上 相等时,在产销平衡表填上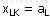 时,产销平衡表的第L行和第K列同时得到满足,为了保证基变量个数为m+n-1个,除了在表上填 时,产销平衡表的第L行和第K列同时得到满足,为了保证基变量个数为m+n-1个,除了在表上填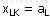 外,必须在表的第L行或第K列某空格(相应运价未被划掉)处填一个“0”,然后同时划去运价表的第L行与第K列。该“0”看作是数字格,即对应的基变量取0值。 外,必须在表的第L行或第K列某空格(相应运价未被划掉)处填一个“0”,然后同时划去运价表的第L行与第K列。该“0”看作是数字格,即对应的基变量取0值。
|

