第二节 表上作业法   (1) (2) (3) (4) (5)
    2.2 最优性检验
    在求出问题的一个可行方案后，就应该判断这个方案是不是最优的。为了进行最优性判别，下面先给出检验数的概念。
    对于空格（i,j），假定给它一个单位运量，调整其他有关数字格运量，则称这一系列变化导致的总运费变化值为该空格的检验数，记作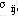。当一个空格的检验数大于零，说明将该空格变为数字格会引起总运量费增加，反之，如果该空格检验数为负值，说明将该空格变为数字格会使总运费降低。因此有以下判别准则：
    定理：如果一个可行方案的所有空格检验数都大于或等于零，则该方案是最优方案。 事实上，按单纯形法，运输问题用非基变量表示的目标函数为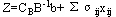 ，显然，单纯形法中的检验数与上述定义的空格检验数是一致的。而运输问题的目标函数是求最小值，自然有上述定理成立。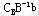对于一个可行方案，只要求出所有空格的检验数，就可以判别该方案是否为最优方案，那么如何求得一个空格的检验数呢？
    下面给出两种计算检验数的方法。
    1.闭回路法
    为了确定空格（i,j）的检验数，可以先找出以该空格为一个顶点，其余顶点全是数字格的闭回路。所谓闭回路，就是从该空格出发，沿水平方向或垂直方向前进，遇到合适的数字格后转90°，继续前进，如果能够回到出发点，则称这个封闭折线为闭回路。然后假定给（i,j）格一个单位运量，调整闭回路上其余数字格的运量，使产销平衡，则闭回路上总运费的变化值就等于（i,j）格的检验数。 可以证明，在任何可行方案中，以空格（i,j）为一个顶点，其余顶点全是数字格的闭回路存在而且唯一。
    比如对例1用最小元素法形成的初始方案，求各个空格的检验数：
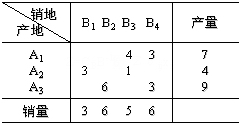
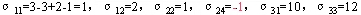