第二节 表上作业法   (1) (2) (3) (4) (5)
    2.3 方案的调整——闭回路法
    当空格的检验数出现负值时，说明当前平衡表给出的调运方案不是最优的，可以进行调整，使总运输费用减少。调整方法如下：
    1°为了使方案有较大改进，先确定最小检验数，即
    2°找出以空格（L，K）为一个顶点，其余顶点全是数字格的闭回路，规定空格（L，K）为闭回路的第一个顶点，闭回路上其它顶点依次为第二个顶点，第三个顶点，…（顺时针或逆时针均可）。取闭回路上偶数序号顶点的最小运量为调整量θ。
    3°闭回路上偶数序号顶点的运量均减θ，奇数序号顶点的运量均加θ，不在闭回路上的运量不变。调整中，如果偶数序号顶点中仅有一个数字格的运量等于θ，则调整后，该格变为空格；如果偶数序号顶点中有两个以上数字格运量等于调整量θ，则调整后，仅让其中一个数字格变为空格，其它调整后要记“0”，表示该格为数字格。经这样调整，就可以得到一个含有m+n-1个数字格的新的调运方案。
    如例1 的初始方案经检验，存在一个负检验数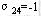，所以， 该方案不是最优方案，在平衡表中找出闭回路下表所示：
    
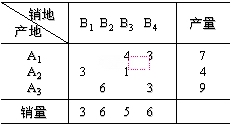
    调整量θ=1，调整后得新方案如下表：
    
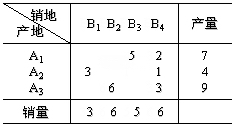
    对新方案的检验结果如下表：
    
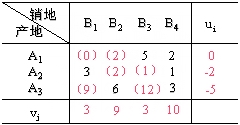
    表中所有检验数均非负，故调整后的新方案已是最优方案。最小总运费为：5×3+2×10+3×1+1×8+6×4+3×5=85（元）