| |
任意事先给定的对画出曲线近似程度的要求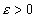 ,可以取 ,可以取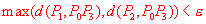 为分裂停止的条件。 为分裂停止的条件。
|
| |
void new_split_Bezier(Point
P[])
{
Point R[4],Q[4];
int i,j;
const double epsilon=0.01;
if(maxdistance(P)<epsilon)
/*maxdistance(P)
为求max(d(P1,P0P3),d(P2,P0P3))的函数*/
{ MoveTo(P[0].x,P[0].y);
LineTo(P[3].x,P[3].y);
} else
{ for(i=0;i<=3;i++)
R[i]=P[i];
for(i=0;i<=2;i++)
{ Q[i]=R[0];
for(j=0;j<=2-i;j++)
{ R[j].x=(R[j].x+R[j+1].x)/2; R[j].y=(R[j].y+R[j+1].y)/2;
} }
Q[3]=R[0];
new_split_Bezier(Q); new_split_Bezier(R);
} }
 有理Bezier曲线 有理Bezier曲线
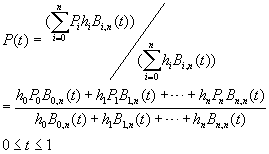
|
|
|
|



