 |
 |
 |
 |
 |
 |
 |
 |
|
 |
|
 |
|
| 第二节 二维形体的表示 | ||||
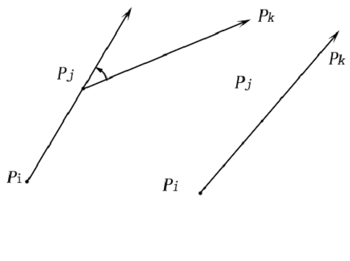 设有曲线上n+1个点的坐标序列,各点依次编号为0,1,2,…,n;为使删去各点距留下前后二点所形成直线的距离不很大而预先给定的阈值  ;为使选出连续三点所成向量夹角不很小而预先给定的阈值 ;参数 表示每次向前检查个点。
1.〔初始化〕 i←0,j←0,k← ,输出点编号0,s←1。{i记最近己选之点,初始起点0为必选,j记待检查之点,算法中保持i≤j,待检查线是点j到k的直线。}2.〔共线性检查〕检查点j到k间各点共线性。若不能通过,距离直线  , 最远的点是m,则k←m返回本步开头。否则继续。{本步必能通过,因最坏在k=j+1时能通过。}3.〔暂定j前后两线方向〕L2←点j到k的方向,若i=j则L1←L2,到6;否则继续。{L2是暂定找到从j向后的新线方向,L1是前次找到原有线方向。} 4.〔向量夹角检查〕检查  ,,三点形成二向量L1和L2的夹角的绝对值,若可以通过即应发生合并,做j←i然后返2,否则继续。{本步检查通过即点j不能选取,而要检查原i到k的直线。}5.〔找到一个选取点〕i←j,L1←点j到k的方向,输出点编号j,s←s+1。 6.〔准备下次〕j←k,k←k+ ,若k>n则k←n,若j≤n-1则返2,否则继续。7.〔最后取点〕输出点编号n,算法结束。 |
||||
 第一节
图形的分段表示第二节
二维形体的表示第三节
四叉树第四节
三维几何模型第五节
分形 |
