 |
 |
 |
 |
 |
 |
 |
 |
|
 |
|
 |
|
| 第五节 分 形 | ||||
 分形的概念
三分康托(Cantor)集 设  是闭区间[0,1],即是满足0≤x≤1的实数x组成的点集; 是去掉中间1/3之后的点集,即是两个闭区间[0，1/3]和[1/3，2/3]; 是分别去掉中两个区间的中间1/3之后的点集,即已经是四个闭区间。此过程要继续进行, 是 个长度为 的闭区间组成的点集。三分康托集F是属于所有的的点组成的集,即
。F可以看成是集序列 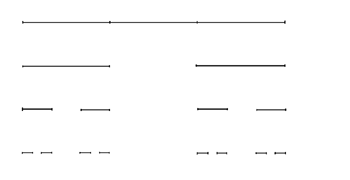当k趋于无穷时的极限。只能画出k取定时的某个。当k充分大时,是对F的很好的近似的表现。
三分康托集是区间[0,1]中的可以展成以3为底的幕级数的下面形式的数组成的: 
其中  的取值限制为0或2,不取1。为看清这一事实,注意从得到时,去掉的是 的数,从得时,去掉的是 的数,并以此类推。三分康托集具有的一些值得注意的特征,这些特征对许多其它的分形也是大体上适合的。 (1) F是自相似的。 的两个区间[0，1/3]，[1/3，2/3]的每一个,其内部F的部分与F整体相似,相似比为1/3。(2) F具有“精细结构”，即它包含有任意小比例的细节。 (3) F的实际定义是简单的和明确的。 (4) 传统的几何学很难描述F的性质,因为F不是满足某些简单条件的点的轨迹,也不是任何简单的方程的解的集合。 (5) F的局部几何性质也很难描述,在它的每点附近都有大量被各种不同间隔分开的其它点。 (6) 按传统几何学中的长度概念,F的长度为零。就是说,尽管从不可数集合这点上说F是一个相当大的集,但它却没有长度,或者说长度不能对F的形状或大小提供有意义的描述。 |
||||
 第一节
图形的分段表示第二节
二维形体的表示第三节
四叉树第四节
三维几何模型第五节
分形 |
