 |
 |
 |
 |
 |
 |
 |
 |
|
 |
|
 |
|
| 第五节 分 形 | ||||
von
Koch曲线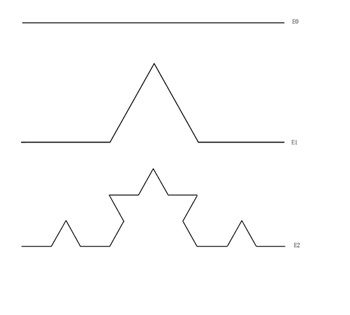 
称集合F是分形,即认为它具有下面典型的性质: (1) F具有精细的结构，即有任意小比例的细节。 (2) F是如此的不规则以至它的整体和局部都不能用传统的几何语言来描述。 (3) F具有某种自相似的形式,可能是近似的或是统计的。 (4) 一般地,F的“分形维数”大于它的拓扑维数。 (5) 在大多数令人感兴趣的情形下,F以非常简单的方法定义,可能由迭代产生。 考虑一个简单的几何图形,取一个边长为1的正方形,若每边扩大2倍,则正方形面积放大4倍,其数学表达式为  =4,这是2维图形。对3维图形,如考虑边长为1的立方体,令每边长放大2倍,则立方体体积扩大8倍,其数学表达式为 =8。类似地,对一个  维的几何对象,若每边长扩大L倍,则这个几何对象相应地放大K倍,归纳前述结果,,L,K三者间的关系式应为:
解出,有:
=lnK/lnL 这里 不必是整数。这就是Hausdorff引人的维数概念,可以称为Hausdorff维数。
|
||||
 第一节
图形的分段表示第二节
二维形体的表示第三节
四叉树第四节
三维几何模型第五节
分形 |
