 |
 |
 |
 |
 |
 |
 |
 |
|
 |
|
 |
|
| 第四节 三维几何模型 | ||||
 面面是二维元素，是形体上一个有限、非零的区域，它由一个外环和若干个内环所界定。面有方向性，一般用其外法向量作为该面的正向。若一个面的外法向量向外，此面为正；否则，为反向面。 体体是三维几何元素，由封闭表面围成的空间，它是欧氏空间R3中非空、有界的封闭子集，其边界是有限面的并集。在实际应用中，要求形体是正则形体，即形体上任意一点的足够小的邻域在拓扑上应是一个等价的封闭圆。不满足上述要求的形体称为非正则形体。存在悬面、悬边的形体是非正则形体。 体素体素是可以用有限个尺寸参数定位和定型的体，常有下面三种定义形式。 一组单元实体 长方体、圆柱体、圆锥体、球体。 扫描体 由参数定义的一条（一组）截面轮廓线沿一条（一组）空间参数曲线作扫描运动而产生的形体。 用代数半空间定义的形体，在此半空间中点集可定义{(x,y,z)|f(x,y,z) 0}此处的f应是不可约的多项式。 形体的层次结构 点→边→环→面→外壳→形体。 在几何造型中最基本的几何元素是点（V）、边(E)、面(F),这三种元素一共有九种连接关系。  |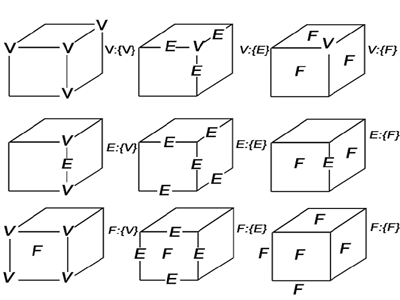
||||
 第一节
图形的分段表示第二节
二维形体的表示第三节
四叉树第四节
三维几何模型第五节
分形 |
