 |
 |
 |
 |
 |
 |
 |
 |
|
 |
|
 |
|
| 第五节 分 形 | ||||
 von
Koch曲线 其源形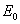  可以是一条线段,
记其端点坐标为 。在算法步1,应令 ,在算法步2,需要依据
,计算图中 三点的坐标。这样m=4,分别得到四个部分图形是  。在算法步3,可画出四条线段 ,擦去前次画线时可能画出的 部分。Von
Koch算法 利用自相似变换来绘制分形 设D是欧氏空间  的闭子集,映射S:D→D称为是D上的压缩，如果对所有D上的点x,y,存在一个数c,0<c<1,能使|S(x)-S(y)|≤c|x-y|。如果其中等号成立,即若|S(x)-S(y)|=c|x-y|,则S把一个集变成了它的几何相似集,此时映射S称为是相似的。设  是压缩,称D的子集F对变换是不变的,如果
三分康托集的情形,这时令  是R→R的变换,分别由
和 的坐标是(0,0)和(1,0),则可以计算求出 的坐标是
自相似变换  和 是平面变换,可一般地设变换矩阵为:
|
||||
 第一节
图形的分段表示第二节
二维形体的表示第三节
四叉树第四节
三维几何模型第五节
分形 |
