 |
 |
 |
 |
 |
 |
 |
 |
|
 |
|
 |
|
| 第五节 分 形 | ||||
 绘制von
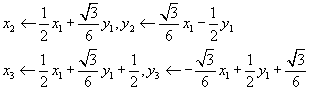Koch曲线 1.〔初始化〕  ←0, ←0,s←1,u←1;{ 为初始点。}2.〔变换〕  3.〔画点〕在显示表面画点  和 ;4.〔存贮〕  ←, ←,s←s+2;5.〔准备下次〕 ← ,u←u+1;6.〔是否结束〕若u>k则算法结束,否则返步2。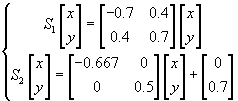 
上面的变换能产生很紧松树树枝的图象。 Julia和Mandelbrot集
设有复数域上如下形式的二次函数:  其中c是复数值常数,做迭代操作: 
研究的问题是: 1.给定  ,当参数c在什么范围内取值能保证 有界2.当c给定,如何选取 ,使有界?
上述迭代,当c=0时,可以有以下三种情况: 1. 序列中的数按模来说越来越小,且趋于零。这时说零是  的吸引子。所有与坐标原点相距小于1的点都产生趋向零的序列。2. 序列中的数按模来说越来越大,且趋向无穷,这时"无穷"也称为过程的吸引子。与坐标原点的距离超过1的所有点都产生趋向无穷的序列; 3. 距坐标原点为1的点,序列总是产生在上面两个吸引区域之间的边界上,此时边界恰为复平面上的单位圆周。 对于上述迭代,当c≠0时,吸引子不再是零,吸引区域的边界不再是光滑的,而是具有自似形的分形结构,这种边界称为Julia集。 |
||||
 第一节
图形的分段表示第二节
二维形体的表示第三节
四叉树第四节
三维几何模型第五节
分形 |
