 |
 |
 |
 |
 |
 |
 |
 |
|
 |
|
 |
|
| 第五节 分 形 | ||||
在复平面上，使 的迭代过程成为有界的复参数c的集合叫做Mandelbrot。设复平面上的迭代过程是:  分离实部和虚部,记 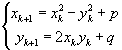 ,有
设计算机显示屏幕的图形分辨率是a×b点,可显示颜色是k+1种,以数字0到k表示,0表示黑色。取定p和q的值,考虑平面上每一点(x,y),探讨吸引区域的结构及其边界即Julia集。 1.〔选定参数〕  ,并令 {这里
区域是考查的复平面范围,M是指定的一个阈值,超过它算是已达到无穷;K是可显示颜色的数目}2.〔逐点着色〕对所有点  ,完成以下循环后算法结束。
2.1〔置初值〕  2.2〔一次迭代〕  2.3〔判断〕 
。若r>M,则选择颜色k,转步2.4; 若k=K,则选择颜色0,即黑色,转步2.4; 若r≤M且k<K,则返回步2.2; 2.4〔一点着色〕对点  着颜色k,对
的下一点,返回步2.1。固定点(x,y),在不同的p和q值之下追踪其迭代点列,在(p,q)平面上记录结果,从而产生Mandelbrot集。设要考查的(p,q)平面范围是-2.25<p<0.75, -1.5<q<1.5,对计算机显示屏幕的假定如前。实施步骤为: 1.〔选定参数〕 
并令 {这里
区域是考查的复平面范围,M是指定的一个阈值;K是显示颜色的数目}2.〔逐点着色〕对所有点  完成以下循环后算法结束。
2.1〔置初值〕 
2.2〔一次迭代〕 
2.3〔判断〕  。若r>M,则选择颜色k,转步2.4; 若k=K,则选择颜色0,即黑色,转步2.4; 若r≤M且k<K,则返回步2.2; 2.4〔一点着色〕对点  着颜色k,对的下一点,返回步2.1。 |
||||
 第一节
图形的分段表示第二节
二维形体的表示第三节
四叉树第四节
三维几何模型第五节
分形 |
