 |
 |
 |
 |
 |
 |
 |
 |
|
 |
|
 |
|
| 第二节 多边形网的明暗处理 | ||||
| 多边形网方法是指用若干多边形表面去拟合任意形状复杂形体的方法。
对用多边形网方法表现的任意形体，形成明暗有三种基本的方法，即常数明暗法（均匀着色法）、亮度插值明暗法（Gouraud着色方法）及法向量插值明暗法（Phong着色方法）。 
1．常数明暗法 常数明暗法又称均匀着色法，就是对每个多边形表面，整个地用一个亮度值（或颜色值）。应用这种方法，应该有以下假设成立： (1) 光源在无穷远处。多边形表面上的任意点的N.L是常数。 (2) 观察者在无穷远处。多边形表面上的任意点的R.V也是常数。 (3) 该多边形表面代替了被模拟的真实表面，而并不是对一个曲面的近似。 最后那个假设常常会产生较大误差。这时用来逼近曲面的各多边形表面可能会被分辨出来。由于每个小面与其相邻的小面在亮度上常有差别，所以在显示图形时就能看到这种差别，这种差别由于Mach带效应而得到加强。Mach带效应指的是当亮度发生不连续的突然变化时，看上去会有一种边缘增强的感觉。视觉上会感到边缘的亮侧更亮，暗侧更暗。Mach带效应是一种由人类视觉系统加工处理而产生的一种感受现象。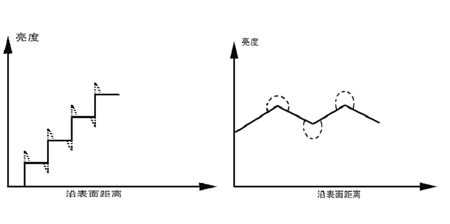 
2．Gouraud方法 亮度（或颜色）插值明暗法 通常被称为Gouraud着色方法。增加逼近空间形体的多边形表面的数目，Mach带效应可以随之减弱。 亮度（或颜色）插值明暗法处理过程有以下四个步骤： (1) 计算各多边形表面的法向量。 |
||||
 第一节
漫反射及具体光源的照明第二节
多边形网的明暗处理第三节
阴 影第四节
纹 理第五节
整体光照明模型第六节
光线跟踪第七节
辐射度方法第八节
色彩模型 |