第三节 直线相关与回归分析的关系
一、直线回归与相关的区别和联系
回归与相关是两个既有区别又有联系的统计分析方法,若研究目的是想定量地描述两个变量间的依存关系,常用来由一个变量的数值去推算另一个变量的数值,则应作回归分析;若目的是想定量地描述两个变量间互依关系的密切程度和方向,则应作相关分析。
㈠ 区别
1. 资料要求不同 回归要求应变量Y 服从正态分布,X 是可精确测量或严格控制的变量,一般称I
型回归。相关要求两个变量服从双变量正态分布,此时若作回归分析,称II 型回归。
2. 分析目的不同 回归用来描述两个变量间的依存关系,相关用来描述两个变量间的互依关系。
㈡ 联系
1. 符号相同 对一组数据若同时计算r 与b , 它们的正负号相同。 r 为正说明两个变量间的相互关系是同向变化的;b
为正说明X 增(减)一个单位,Y 平均增(减) b 个单位。
2. 假设检验等价 对同一样本,样本回归系数b 的t 检验与样本相关系数r 的t 检验的t
值相等,即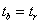 。由于b
的假设检验较繁,故在实际应用中常用r 的t 检验代替。 。由于b
的假设检验较繁,故在实际应用中常用r 的t 检验代替。
3. 用回归解释相关 r 的平方称为决定系数(coefficient of determination)
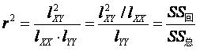 公式(13.10)
公式(13.10)
上式说明当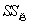 固定不变时,回归平方和 固定不变时,回归平方和 的大小决定了 的大小决定了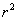 的大小。 的大小。 越接近 越接近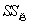 ,则 ,则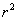 越接近1,则回归效果越好。 越接近1,则回归效果越好。
二、应用相关分析的注意事项
1. 作相关分析要有实际意义 不能把毫无关联的两个事物或现象拿来作相关分析。
2. 相关关系不一定是因果关系 因果关系需根据专业知识证明,相关分析有助于寻找事物的原因。
3. 相关系数的大小不能说明两事物或现象存在相关关系 推断两个事物或现象之间有无直线相关关系,必须进行相关系数的假设检验。 |
|


