第一节 整数规划问题     (1) (2)
    解：设x1,x2分别表示甲、乙货物托运的件数（整数），则该问题的数学模型为：
        
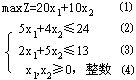
    这里货物的件数只能是整数，所以这是一个纯整数规划。若先不考虑整数限制， 可求得问题的最优解为：x1=4.8，x2=0， maxZ=96 由于x1=4.8不符合整数要求，所以该解不是整数规划的最优解。
    是否可以将非整数解用“四舍五入”方法处理呢？事实上，如果将x1=4.8，x2=0近似为x1=5，x2=0，则该解不符合体积限制条件⑵： 5x1+4x2≤24 因而它不是最优解；
    那么用“舍尾取整”方法处理又如何呢？将x1=4.8，x2=0 “舍尾取整”为x1=4，x2=0，显然满足各约束条件，因而它是整数规划问题的可行解，但它不是整数最优解。因为它对应的目标函数值Z=80，而x1=4，x2=1这个解亦是可行解，但它对应的目标函数值Z=90。
    由此例看出，简单的处理方法常常得不到整数规划的最优解，甚至得不到可行解。
    如何求得这类问题的整数最优解呢？到目前为止，整数规划还没有一种很满意的和有效的解法。现在用以求解整数规划的方法基本都是将整数规划变为一系列线性规划来求解的。我们将介绍两种方法——分枝定界法和割平面法。