第三节
割平面法 (1)
(2) (3)
割平面法是1958年美国学者R.E.Gomory提出的求解纯整数规划的一种比较简便的方法,其基本思想是:先不考虑变量的整数限制求解线性规划,如果得到的解不是整数解,则不断增加适当的约束,割掉原可行域不含整数解的一部分,最终得到一个具有若干整数顶点的可行域,而这些顶点中恰有一个顶点是原问题的整数解。
割平面法的基本步骤:
步骤1 不考虑变量的整数限制,求解相应的线性规划问题,如果该问题无解,或最优解已是整数解,则停止计算,否则转下一步。
步骤2 对上述线性规划的可行域进行“切割”,去掉不含整数解的一部分可行域,即增加适当的线性约束,然后转步骤1。
割平面法的关键在于如何确定切割方程,使之能对可行域进行真正的切割,而且切去部分不含有整数解点。
下面讨论切割方程的求法。
设与整数规划相对应的线性规划最优解中基变量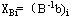 不是整数,将最优单纯形表中该基变量对应的行还原成约束方程,即 不是整数,将最优单纯形表中该基变量对应的行还原成约束方程,即
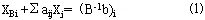
将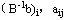 都分解成整数与非负真分数之和的形式,即 都分解成整数与非负真分数之和的形式,即

这里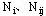 是整数,将⑵、
⑶代入⑴,得 是整数,将⑵、
⑶代入⑴,得
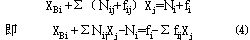
当诸Xi都是整数时, ⑷式左端是整数,所以右端亦应是整数,但右端是两个正数之差,且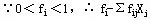 是小于1的整数, 是小于1的整数,
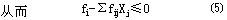
取⑸式作为切割方程。因为任何整数可行解都满足这个方程,所以把它加到原问题的约束中,它能够对原可行域进行切割,而不会切割掉整数解。
|

