第三节
割平面法 (1)
(2) (3)
将新约束方程加到原最优表下面(切割),求得新的最优解如下 :
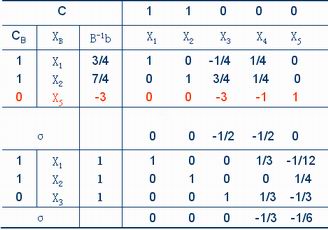
由于X1,X2的值已是整数,所以该题经一次切割已得最优解:
X1=1,X2=1,最优值: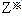 =2 =2
现在我们来看看切割方程 3X3+X4 ≥3 的几何意义。
例3对应的线性规划为
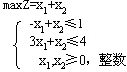
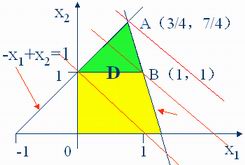
用图解法求得可行域D及最优解点A,见下图:
由标准化的约束方程组可得
X3=1+X1-X2
X4=4-3X1-X2
代入切割方程 得 3(1+X1-X2)+(4-3X1-X2)≥3
即X2≤1,将此切割方程 加入原约束中,就等于切掉原可行域得A1B部分,如图。显然在A1B区域不含整数解点,对原可行域切割的结果是产生了一个新顶点B,用图解法在新的可行域(黄色)中可求得整数最优解恰是B(1,1)。
在求解实际问题中,割平面法经常会遇到收敛很慢的情况,但若和其它方法,如分枝定界法,联合使用,一般能收到比较好的效果。
|

