第二节
动态规划的基本概念和最优化原理 (1)
(2) (3)
从上面的例子不难看出,对于最短线路问题,有如下的递推关系(函数方程):
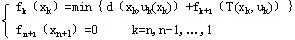
一般情况下,多阶段决策问题存在下面的递推关系:
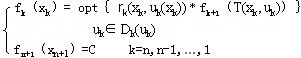
这里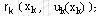 是第阶段采用 是第阶段采用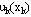 决策产生的阶段效应; 决策产生的阶段效应;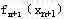 =C是边界条件;“﹡”号大多数情况下是
“+”号,也可能是“×”号。称上述递推关系为动态规划的基本方程,这个方程是最优化原理的具体表达形式。 =C是边界条件;“﹡”号大多数情况下是
“+”号,也可能是“×”号。称上述递推关系为动态规划的基本方程,这个方程是最优化原理的具体表达形式。
在基本方程中,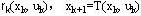 都是已知函数,最优子策略 都是已知函数,最优子策略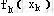 与 与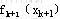 之间是递推关系,要求出 之间是递推关系,要求出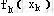 及 及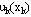 ,需要先求出 ,需要先求出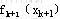 ,这就决定了应用动态规划基本方程求最优策略总是逆着阶段的顺序进行的。 ,这就决定了应用动态规划基本方程求最优策略总是逆着阶段的顺序进行的。
另一方面,由于k+1阶段的状态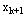 =T( =T(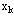 , ,
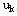 )是由前面的状态和决策所形成的,在计算 )是由前面的状态和决策所形成的,在计算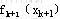 时还不能具体确定 时还不能具体确定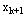 的,这就要求必须就k+1阶段的各个可能状态计算 的,这就要求必须就k+1阶段的各个可能状态计算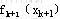 ,因此动态规划不但能求出整个问题的最优策略和最优目标值,而且还能求出决策过程中所有可能状态的最优策略及最优目标值。 ,因此动态规划不但能求出整个问题的最优策略和最优目标值,而且还能求出决策过程中所有可能状态的最优策略及最优目标值。
|

