第三节
建立动态规划数学模型的步骤 (1)
(2) (3) (4)
“最优化原理”是动态规划的核心,所有动态规划问题的递推关系都是根据这个原理建立起来的,并且根据递推关系依次计算,最终可求得动态规划问题的解。
一般来说,利用动态规划求解实际问题需先建立问题的动态模型,具体步骤如下:
⒈将问题按时间或空间次序划分成若干阶段。有些问题不具有时空次序,也可以人为地引进时空次序,划分阶段。
⒉正确选择状态变量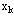 。这一步是形成动态模型的关键,状态变量是动态规划模型中最重要的参数。一般来说,状态变量应具有以下三个特性: 。这一步是形成动态模型的关键,状态变量是动态规划模型中最重要的参数。一般来说,状态变量应具有以下三个特性:
⑴要能够用来描述决策过程的演变特征。
⑵要满足无后效性。即如果某阶段状态已给定后,则以后过程的进展不受以前各状态的影响,也就是说,过去的历史只通过当前的状态去影响未来的发展。
⑶递推性。即由k阶段的状态变量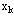 及决策变量uk可以计算出k+1阶段的状态变量 及决策变量uk可以计算出k+1阶段的状态变量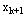 。 。
⒊确定决策变量及允许决策变量集合Dk(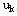 )。 )。
⒋根据状态变量之间的递推关系,写出状态转移方程: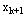 =T(
=T(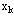 , ,
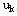 ( (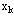 )) ))
⒌建立指标函数。一般用rk(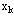 , ,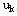 )描写阶段效应,fk(
)描写阶段效应,fk(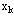 )表示k—n阶段的最优子策略函数。 )表示k—n阶段的最优子策略函数。
⒍建立动态规划基本方程:
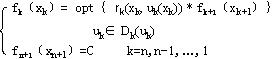
以上是建立动态规划模型的过程,这个过程是正确求解动态规划的基础。 |

