第三节
建立动态规划数学模型的步骤 (1)
(2) (3) (4)
在动态规划基本方程中,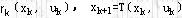 都是已知函数,最优子策略 都是已知函数,最优子策略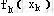 与 与
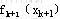 之间是递推关系,要求出 之间是递推关系,要求出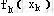 及 及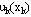 ,需要先求出 ,需要先求出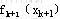 ,这就决定了应用动态规划基本方程求最优策略总是逆着阶段的顺序进行的。由后向前逐步计算,最终可以算出全过程的最优策略函数值及最优策略。 ,这就决定了应用动态规划基本方程求最优策略总是逆着阶段的顺序进行的。由后向前逐步计算,最终可以算出全过程的最优策略函数值及最优策略。
另一方面,由于k+1阶段的状态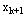 =T( =T(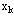 , ,
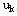 )是由前面的状态 )是由前面的状态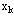 和决策 和决策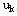 所形成的,在计算 所形成的,在计算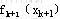 时还不能具体确定的
时还不能具体确定的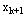 值,所以,这就要求必须就k+1阶段的各个可能状态计算 值,所以,这就要求必须就k+1阶段的各个可能状态计算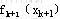 ,因此动态规划方法不但能求出整个问题的最优策略和最优目标值,而且还能求出决策过程中所有可能状态的最优策略及最优目标值。 ,因此动态规划方法不但能求出整个问题的最优策略和最优目标值,而且还能求出决策过程中所有可能状态的最优策略及最优目标值。
下面就按上述步骤求解例2。
例2(带回收的资源分配问题)某厂新购某种机床125台。据估计,这种设备5年后将被其它设备所代替。此机床如在高负荷状态下工作,年损坏率为1/2,年利润为10万元;如在低负荷状态下工作,年损坏率为1/5,年利润为6万元。问应如何安排这些机床的生产负荷,才能使5年内获得的利润最大?
解:以年为阶段,k=1,2,3,4,5, 取k年初完好的机床数为状态变量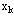 ,
以k年初投入高负荷运行的机床数为决策变量 ,
以k年初投入高负荷运行的机床数为决策变量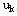 ,则低负荷运行机床数是 ,则低负荷运行机床数是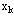 - -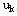 ,于是状态转移方程为: ,于是状态转移方程为:
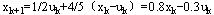
以利润为目标函数,则k年利润为:
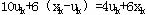
记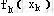 为k年至5年末最大总利润,则动态规划基本方程为: 为k年至5年末最大总利润,则动态规划基本方程为:
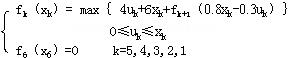
|

