节导航

章导航

第二节 精度的概念及衡量精度的数字指标


从前面的分析可以知道，测量成果中会不可避免地含有误差。但测量成果只有符合《规范》规定的限差要求时，才算合格，否则应重测。


一、精度与观测质量
高斯分布曲线有一个峰顶和两个拐点，当△=0时，密度函数有最大值 ；两个拐点的横坐标值为
（7）
由于横轴和其垂线 ， 所包围的曲边体形面积，是误差落在区间（-σ，+σ）的概率，为一定值，所以当参数σ 的绝对值愈小时，曲线愈陡峭，表示误差的分布愈密集；反之，当参数σ 的绝对值愈大时，曲线愈平缓，表示误差的分布愈离散。
精度：误差分布的密集或离散的程度，称为“精度”。
精度高，表示误差分布密集，反映了观测条件好、观测质量高；反之，精度低，表示误差分布离散，反映了观测条件差、观测质量低。因此，精度可用来衡量观测质量的好坏，是测量上的一个重要概念（图2-1）。
要特别注意，精度所反映的是在一定的观测条件下，真误差群体的分布状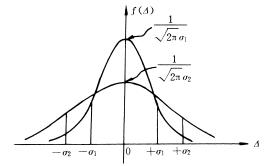
图2-1 误差分布
况，而绝不是个别真误差的大小。它描述了观测条件的好坏和观测质量的高低。


二、衡量精度的指标--中误差
1.中误差m
高斯分布密度函数中的参数σ，在几何上是曲线拐点的横坐标，概率论中称为随机变量的标准差（方差的平方根）。当观测条件一定时，误差分布状态唯一被确定，误差分布曲线的两个拐点也唯一被确定。用σ作为精度指标，可以定量地衡量观测质量。所以在衡量观测精度时，就不必再作误差分布表，也不必绘制直方图，只要设法计算出该组误差所对应的标准差σ值即可。
σ的平方称为方差σ2 ，在概率论中有严格的定义：方差σ2是随机变量x与其数学期望E(x)之差的平方的数学期望，用数学公式表达就是
（8）
用测量专业的术语来叙述标准差σ：在一定观测条件下，当观测次数n无限增加时，观测量的真误差△的平方和的平均数的平方根的极限，由下式表示：
（9）
式中 为真误差 的平方和，等价于 ， 。
通常，观测次数n总是有限的，只能求得标准差的“估值”，记作m，称为“中误差”。其值可用下式计算：
（10）
由中误差的定义可知，中误差m不等于每个测量值的真误差，它只是反映这组真误差群体分布的离散程度大小的数字指标。
2.平均误差θ
定义：在一定观测条件下，当观测次数n无限增加时，真误差绝对值的理论平均值的极限称为平均误差，记作
（11）
因观测次数n总是有限的，故其估值表示：
（12）
式中 为真误差绝对值之和。
3.或然误差ρ
在一定观测条件下，当观测次数n无限增加时，在真误差列中，若比某真误差绝对值大的误差与比它小的误差出现的概率相等，则称该真误差为或然误差，记作ρ。
因观测次数n有限，常将ρ的估值记作ω。或然误差ω可理解为：将真误差列按绝对值从大到小排序，当为奇数时，居中的真误差就是ω；当为偶数时，居中的两个真误差的平均值作为ω。
平均误差、或然误差与中误差有如下关系：
θ≈0.7979m
ω≈0.6745m
作为精度指标，中误差最为常用，因为中误差更能反映误差分布的离散程度。
例[1] 设对某个三角形的内角用两种不同精度的仪器各进行了10次观测，求得每次观测所得的三角形内角和的真误差为
Ⅰ列：+3″，-4″，-3″，+4″，-5″，-2″，+3″，+3″，-4″，+5″
Ⅱ列：-1″，0″，+12″，0″，-1″，-10″，+1″，0″，+1″，-10″
试求其观测精度。
解：
1.用中误差公式计算


2.用平均误差公式计算


3.用或然误差公式计算
按绝对值将误差列由大到小排序，即
Ⅰ列：5″，5″，4″，4″，4″，3″，3″，3″，3″，2″
Ⅱ列：12″，10″，10″，1″，1″，1″，1″，0″，0″，0″


计算结果表明：用中误差衡量观测精度，第一列高于第二列，符合客观实际，因第二列中有+12″，-10″，-10″三个大的误差存在，误差分布离散。很显然，用平均误差和或然误差来衡量观测精度，在本例均未有效地反映实际情况。


三、限差
在一定观测条件下，误差不会超出一定的限值。当误差超过限差时，就认为观测结果不符合要求，应舍去。我们称这样的限值为限差。
理论及实验研究表明，误差落在区间（－kσ，+kσ）的概率为
k=1时， P（△）≈68.3%；
k=2时， P（△）≈95.5%；
k=3时， P（△）≈99.7%。
由此可见：误差大于2倍中误差时，出现的概率仅为4.5%；误差大于3倍中误差时，出现的概率为0.3%。由于大于2倍中误差的偶然误差出现的机会已很小，因此测量工作中常取2倍中误差作为误差的限值，称为测量成果取舍的限差，也称容许误差，即
△限=2m （13）
在测量工作中，真误差、中误差和容许误差都称为绝对误差。


四、相对误差
在进行精度评定时，有时仅利用绝对误差还不能反映测量的精度。因为有些量，如长度，用绝对误差不能全面反映观测精度。
定义：绝对误差与测量值之比，记作K。习惯上相对误差用分子为1的分数表达，分母越大，相对误差越小，测量的精度就越高。
例[2] 用同一把已检定过的钢尺分别丈量两条边，长度分别为30m和90m，其中误差（绝对误差）均为±10mm。试衡量其测量精度。
解：若用绝对误差衡量测量精度，因m1=m2=±10mm，无法判别那条边长丈量的精度更高。现计算相对误差，有


即第二条边丈量精度高于第一条边。距离测量中常用相对误差衡量测量精度。