Distant Education College of JiLin Univercity
第6章 测量误差基本知识
(一)学习目标: 测量工作除了要提供可靠的成果外,还需要对测量成果的精度进行描述。学习本章内容就是为了客观、准确地对成果的精度进行评定和分析。掌握测量误差及数据处理的基本知识,做好测量实施前的技术准备,达到限制测量误差,处理测量数据,提高观测成果的精密度、准确度和置信度具有重要的意义。
1.了解系统误差、偶然误差的特征和相应处理方法。
2.能够运用误差传播定律计算观测值函数的中误差。
3.掌握算数平均值、带权平均值及其中误差的计算。
4.学会运用真误差、似真差计算中误差评定观测值的精度。
5.了解最小二乘法原理。
(二)主要知识点:
第一节 测量误差的概念、来源和分类,偶然误差的特性
一、测量误差的定义
在测量工作中,观测者无论使用多么精良的仪器,操作如何认真,最后仍得不到绝对正确的测量成果,这说明在各观测值之间或在观测值与理论值之间不可避免地存在着差异,我们称这些差异为观测值的测量误差。
设某观测量的真值为X表示。若以li(i=1,2,…,n)表示对某量的n次观测值,并以△表示真误差,则真误差可定义为观测值与真值之差,即
![]()
![]() (1)
(1)
若用xi 表示X的估值, vi表示改正数,则
xi =li+ vi vi = xi -li
二、测量误差的产生
测量工作是在一定的条件下进行的,一般来说,外界环境、测量仪器和观测者构成观测条件。而观测条件不理想或不断变化,是产生测量误差的根本原因。
1.外界环境
主要指观测环境中气温、气压、空气湿度和清晰度、大气折光、风力等因素的不断变化,会导致观测结果中带有误差。
2.仪器误差
(1)仪器制造误差
(2)检校残余误差
3.观测误差
观测者的感官的鉴别能力、技术熟练程度和劳动态度等也会产生误差。可见,观测条件不可能完全理想,测量误差的产生不可避免。但是,在测量工作实践中,可以采取一定的措施和方法来改善乃至控制观测条件,从而能够控制测量误差。 综上所述,观测结果的质量与观测条件的优劣有着密切的关系。观测条件好,观测误差就可能会小一些,观测质量相应地会高一些;反之,观测结果的质量就会相应降低。当观测条件相同时,可以认为观测结果的质量是相同的。于是,我们称在相同条件下所进行的一组观测为等精度观测,而称在不同条件下所进行的一组观测为非等精度观测。
三、测量误差的分类
测量误差按性质可分为两类:一类为系统误差;另一类为偶然误差(又称随机误差)。此外,还有属于错误性质的“粗差”。
1.系统误差
在相同观测条件下,对某量进行一系列观测,若误差的数值和正负号按一定规律变化或保持不变(或者误差数值虽有变化而正负号不变),具有这种性质的误差称为系统误差。
例如,用一支名义长度为30m,而经检定后,其实际长度为29.99m的钢尺来量距,则每量30m的距离,就会产生1cm的误差,丈量60m的距离,就会产生2cm的误差。
性质:这些误差在测量成果中具有累积性,对测量成果质量的影响较为显著。
减弱措施:由于这些误差具有一定的规律性,所以,我们可以通过加入改正数或采取一定的观测措施来消除或尽量减少其对测量成果的影响。总之,通过采取相应的措施,可以将系统误差消除或减少到可以忽略不计的程度。
2.偶然误差
在相同观测条件下,对某量进行一系列观测,若误差的取值有多种可能,其数值和正负号均无法确定。即,就误差列中的单个误差来看,其数值和正负号没有规律性,但从误差列的总体来观察,则具有一定的统计规律,这种误差称为偶然误差,又称随机误差。
例如,用经纬仪测角时,用望远镜瞄准目标时产生的照准误差;水准测量时,瞄准水准尺估读毫米的读数误差等,都属于偶然误差。
性质:是服从或近似服从正态的随机误差。
偶然误差是由观测条件受到诸多无法预料的因素影响所致。偶然误差,就个别值而言,在数值和正负号上确实无规律可循,是无法预知的。在测量工作中,我们只能靠选择合适的仪器、合理的操作方法和认真负责的态度,在较好的外界条件下进行观测,以减小偶然误差的影响,而无法将其完全消除。
在观测过程中,系统误差和偶然误差总是相伴而生的。当系统误差占主导地位时,观测误差就呈现一定的系统性;反之,当偶然误差占主导地位时,观测误差就呈现偶然性。如前所述,系统误差有明显的规律性,容易发现,也较易控制,所以在测量过程中总可以采取各种办法消除其影响,使其处于次要地位。而偶然误差则不然,不能完全消除,故本章中所讨论的测量误差,均系指偶然误差而言。
3.粗差
粗差是测量中的疏忽大意而造成的错误或电子测量仪器产生的伪观测值。
粗差非常有害,会对工程造成难以估量的损失。所以,应尽早将粗差剔除。
四、偶然误差的特点
如上节所述,偶然误差的产生受多种因素的影响,难以消除。因而,偶然误差便成为误差理论中最核心的内容和主要的研究对象。
(一)观测实验与偶然误差的分布
实验:相同观测条件下,独立地观测217个三角形的全部内角,由于观测结果中存在偶然误差,三角形的三内角观测值之和不等于其理论值180°,由式(1)可求得每个三角形三内角和的真误差(又称三角形闭合差,属偶然误差),即 ![]()
![]() (2)
(2)
式中,△i 表示第i个三角形的闭合差,[l ]i 表示第i个三角形三内角之和,符号“[ ]”为高斯求和符号,等价于“∑ ”。
分析:将217个真误差分成正误差和负误差两类,并分别按绝对值大小,从小到大排序。最后,取误差区间为d△=3″,统计落在各区间正负误差的个数ni和真误差落在某区间这一事件的频率为 ni /N ,N为真误差总数,即N = 217。统计时将等于区间上限的真误差统计在下一个区间内,如△=3″不属第一区间
0″到+3″,而属第二区间+3″到+6″。
可看出:误差出现的频率与误差大小有关,即绝对值小的误差出现的频率较大,而绝对值大的误差出现的频率较小;在各区间内,正误差和负误差的个数相近,且正误差的总个数(108)和负误差的总个数(109)几乎相等;真误差的绝对值不会超过某一定值(本次实验为27″)等。
若以横坐标表示真误差大小,以纵坐标表示真误差在各区间的分布密度(频率除以误差区间长,即(ni / N)/ d△)。可以画为真误差分布图(图1-1),又称直方图。直方图可以更形象地表达217个真误差的分布状态。
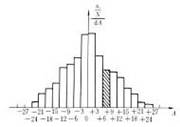
图1-1 直方图
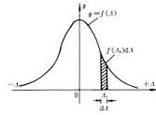
图1-2 正态分布图
(二)偶然误差的统计特性
若我们按照上述方法再做一些测量实验,其测量结果仍会显示出类似的规律。通过大量测量实验统计结果,特别是当观测次数很多时,可总结出偶然误差的如下特性:
(1)在一定观测条件下,偶然误差的绝对值不会超出一定限值(有界性)。
(2)绝对值小的误差比绝对值大的误差出现的机会要多(或称概率大,密集性)。
(3)绝对值相等的正、负误差出现的机会相等(对称性)。
(4)当观测次数n无限增加时,误差的算术平均值(数学期望)趋近于零,即
![]() (3)
(3)
式中,[△]为真误差代数和,即,[△]=△1+△2+……+△n。
上述偶然误差的四个特性具有普遍性,对误差理论的研究和测量实践都有重要意义。
图1-1所反映的误差分布称为经验分布。当观测次数n→∞、误差区间间隔无限缩小时,落在各区间的误差频率ni / N将趋近于其概率P(△i),这时直方图中长方形顶边所形成的折线将变成一条光滑曲线(如图1-2),称为误差的理论分布(或误差分布曲线),这就是概率论中著名的高斯正态分布。
高斯正态分布曲线的纵坐标表示误差分布的概率密度,它是偶然误差的函数,简称概率函数,率密度函数的数学模型为记为f (△)
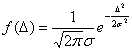 (4)
(4)
式中,横坐标表示误差的大小,曲线下的面积是误差出现的概率,即
![]() (5)
(5)
当观测次数无限增加时,△的所有可能取值均出现,“误差落在误差曲线与横轴所包围的面积内”这个事件是必然事件,误差出现的概率等于1,即
![]() (6)
(6)
