节导航

章导航

第五节 观测值的算术平均值及其中误差


一、观测值的算术平均值
在相同的观测条件下，对某一未知量（如角度或边长）的真值为X，对该量作n次观测，设n次观测值分别为l1、l2、…、ln。
则观测值的真误差为△i（i=1,2,…,n），即

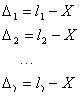
等式两边求和并同除以n，有

（35）
式中 称为“算术平均值”，习惯以x表示；当观测次数无限增加时，根据偶然误差特性（4），式中 趋近于零。于是可得
(36)
在实际工作中，观测次数总是有限的，算术平均值x作为未知量的估值，称为未知量的“最或是值（或称最可靠值）”，它比任何观测值都接近真值。
算术平均值的一般表达式为
（37）
以上所述就是算术平均值原理，它是测量中重要理论之一。


二、算术平均值的中误差
根据算术平均值的计算公式

设各观测值的中误差均为m，1/n为常数，若以mx表示平均值的中误差，则得算术平均值的中误差计算公式为

从而 （38）
即，算术平均值的中误差与观测次数的平方根成反比，或者说，算术平均值的精度比观测值的精度提高了 倍。


三、用改正数计算等精度观测值的中误差
用真误差求观测值的中误差，即

用改正数计算观测值的中误差，即
（39）
式中vi为观测值的改正数。
推导如下：
1）改正数等于独立观测值的最或然值x与观测值li的差，即
（40）
其中，n为观测次数。
2）改正数的性质
∵
将上式两边求和，有

由于 ，代入上式，有 [v]=0
结论：改正数的和恒等于零。这一性质可作为计算的检核。
3）用改正数计算观测值的中误差
由前面已列出的两个关系式，即


以上两式相加，有
式中，△x=x-X为算术平均值x的真误差。由此得观测值的真误差为

上式两边平方后求和，有
（41）
∵[v]=0
∴上式第三项为零，将上式等号两边同除以n，便有
（42）
其中， 是算术平均值的真误差，无法知道，可用

近似代替，将 代入式(35)，得

即，
整理后得
上式即为用改正数来求观测值中误差的公式，称为白塞尔公式。
若将此式代入式（38），则得用改正数计算观测值算术平均值中误差的计算公式为
（43）


四、关于观测次数的讨论
m一定时，随着n的增大，的值不断减小，即x的精度不断提高。但当观测次数增加到一定数目以后，再增加观测次数，精度则提高得很少。可见，一味地增加观测次数并不一定有利。
在测量工作中，观测次数有时称为测回数。如进行光电测距、角度测量时就叫测回数。测回数的定义随观测量不同而不同，如经纬仪测角时，盘左盘右各一次称为一测回；光电测距时，瞄准反射棱镜一次，连续从显示器上读得四个数据称为一测回。在生产实践中，决定观测次数或测回数，主要依据工程要求、仪器精度等因素，有关“规范”均有相应的规定。