 |
 |
 |
 |
 |
 |
 |
 |
|
 |
|
 |
|
| 第二节 多边形表面的交线计算 | |||
若给出空间若干点的坐标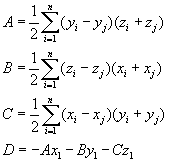 注意这里没有要求这些点共面或围成了凸多边形,都可以求出通过或接近这些点的一个平面方程Ax+By+Cz+D=0:
式中若i=n,则j=1,否则j=i+1  平面方程的求交
两平面重合或平行,一般算没有交点。 分别对每个多边形表面各边相应的线段,计算它与另一个多边形表面所在平面的交点。注意这里是求线段与平面的交点,即交点在线段延长线上时算不相交。假定两个多边形表面都是凸的,故共可以交出四个交点。 线段与平面的交点计算
空间线段两个端点的坐标 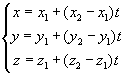 和 给出,平面方Ax+By+Cz+D=0。
代入平面方程,得: 
整理得到: 
于是知道,若  则所给线段在平面上或与平面平行,没有唯一确定的交点。否则,交点对应的参数t可以求出: 
|
|||
 第一节
线段的交点计算第二节
多边形表面的交线计算第三节
平面中的凸壳算法第四节
包含与重叠第五节
简单多边形的三角剖分 |
