 |
 |
|
|
|
| |
|
|
|
|
| |
|
第二节
二维形体的表示 |
|
|
| |
|
|
|
|
| |
设表示要求交两曲线的带树己构造得足够精确,即在树叶一层,来自不同带树的矩形带段或是不相交或是良性相交,而没有可能性相交出现。
两树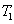 和 和 表示的两条曲线是否相交的算法,可以简略叙述如下: 表示的两条曲线是否相交的算法,可以简略叙述如下:
若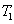 和 和 对应的矩形带段互不相交,那么它们代表的曲线不相交; 对应的矩形带段互不相交,那么它们代表的曲线不相交;
若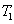 和 和 对应的矩形带段良性相交,那么它们代表的曲线相交; 对应的矩形带段良性相交,那么它们代表的曲线相交;
若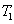 和 和 对应的矩形带段可能性相交,且 对应的矩形带段可能性相交,且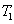 的面积大于或等 的面积大于或等 的面积,那么分别执行 的面积,那么分别执行 与 与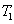 的左右两个儿子结点的相交性检查。 的左右两个儿子结点的相交性检查。
若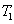 的面积小于 的面积小于 的面积,则把它们位置对换一下再如上进行两个检查。若两个检查的结果都是不相交,则认为所表示曲线不相交;若两个检查中有一个是良性相交,则认为所表示曲线相交;若不是上述两情形,即出现可能性相交,则对可能性相交的两个矩形带段中面积较大者,取其对应结点的两个子结点,如此进行可直到树叶那一层。 的面积,则把它们位置对换一下再如上进行两个检查。若两个检查的结果都是不相交,则认为所表示曲线不相交;若两个检查中有一个是良性相交,则认为所表示曲线相交;若不是上述两情形,即出现可能性相交,则对可能性相交的两个矩形带段中面积较大者,取其对应结点的两个子结点,如此进行可直到树叶那一层。
实践表明用带树方法表示曲线对提高计算效率是有帮助的。另外两个带树对并、交等运算是封闭的,与用象素阵列来表示图形的方法比较空间需求也算是节省的。
|
|
|
|
|



